
Left: Squeezing of a capsule between two plates
Carin et al. 2003, Rachik et al. 2006
Right: Spinning capsule
Pieper et al 1998, Husmann et al. 2005
A capsule consists of an internal medium (pure or complex liquid), enclosed by a deformable membrane. In Biomedical Engineering, bio-artificial capsules are used in drug delivery systems, artificial organs or cell therapy. A liquid filled capsule is also an appropriate model for a simple cell such as a red blood cell.
When capsules are suspended in a flowing liquid, they are deformed by viscous fluid stresses and may sometimes burst. Modeling of this process is necessary for bio-artificial capsule design and control of breakup.
A major issue is the determination of the mechanical properties of the membrane, as these control the resistance of the capsule to applied stresses.
In many cases the membrane is very thin and treated as a two-dimensional solid with hyperelastic or visco-elastic properties. Popular membrane constitutive laws include the Mooney-Rivlin (MR) law that assumes that the membrane is an infinitely thin sheet of a 3D incompressible material. For membranes with a finite area dilation resistance, a Skalak et al. (Biophys. J., 1973) law (SK) or Evans & Skalak (Mechanics and Thermodynamics of Biomembranes. CRC Press.1980) law (ES) are usually preferred as they account separately for shear deformation and area dilatation of the material. However, MR, SK or ES laws lead to quite different membrane behaviors for large deformations (Barthes-Biesel et al. 2002).
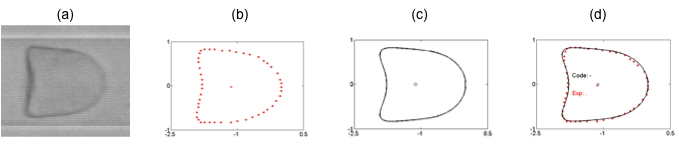
The membrane mechanical properties have to be inferred from experiments such as squeezing a capsule between two plates or spinning a capsule in a tube. Recent experiments have shown that gelatin membranes reinforced with a polymer network, are equally well described by a SK or ES law where the area dilatation and shear modulus are of the same order.

Carin et al. 2003, Rachik et al. 2006
Pieper et al 1998, Husmann et al. 2005
An inverse method is used to characterize the membrane mechanical behavior of liquid filled microcapsules. Cross-linked ovalbumin spherical microcapsules (radius a) are flowed and deformed into a cylindrical microchannel of comparable size (radisus R). The deformed shape is compared to predictions obtained numerically when modeling a capsule under the same flow conditions. The unknown shear modulus value corresponds to the best fit. This method can discriminate between various cross-linking degrees of microcapsules fabricated at different reaction pH and reticulation times (Lefebvre et al. 2008, Chu et al. 2011)
The general problem consists in analyzing the motion of a capsule freely suspended in another liquid subjected to a known flow field in the limit of small Reynolds numbers. The effect of membrane rheology on the capsule response can then be assessed by comparing two capsules subjected to the same flow but with different membrane constitutive laws.
Two free surface flow problems (motion of the internal liquid and of the suspending fluid) and one solid mechanics problem (deformation of the membrane) must be solved simultaneously. An efficient method consists in recasting the Stokes equations in integral form and in using the boundary integral techniquein conjunction with Lagrangian tracking of the position of the membrane material points. A structured mesh on the interface and cubic B-spline functions can be used for interpolation of the various quantities on a boundary element. Recently, an unstructured mesh has been used on the interface and the membrane equlibrium has been solved by measn of the finite element method (Walter et al. 2010).
A capsule is freely suspended in a linear shear flow such as simple shear. The problem consists in determining its motion and deformation and the eventual onset of burst.
From left to right: k<kL ; kL<k<kH ;k>kH. (Lac et al 2004)
Results have been obtained for a capsule freely suspended in unbounded simple shear flow with shear rate k. For an interval of shear rate values kL<k<kH, the capsule elongates until it reaches a steady shape with the major axis inclined with respect to streamlines. The membrane continuously rotates around the steady profile: the well known tank-treading motion, first observed for red blood cells, is thus recovered. It is then possible to predict the value of the deformation, orientation and rotational frequency as a function of shear rate and membrane rheology.
For large values k>kH , the capsule exhibits two tips along the direction of elongation where compressive tensions appear, no equilibrium shapes can be identified and burst is conjectured to occur.
For smalle values k<kL, equilibrium shapes are briefly captured but become unstable due to the development of compressive tensions. These occur in the vicinity of the equator and cause the membrane to fold in a fashion similar to that reported for polysiloxane microcapsules.
However, the folding instability can be removed by first inflating the capsule with osmotic pressure. The necessary level of internal pressure to make the capsule stable depends on the shear rate and on the membrane constitutive behaviour. The effect of initial pre-inflation is also to shift the value of kH to higher shear rates, since the membrane appears more rigid.
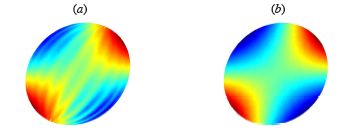
(a) without pre-stress, membrane buckling occurs and the resulting equilibrium shape is unstable.
(b) with pre-inflation, the pre-stress level compensates negative membrane elastic tensions and prevents buckling (Lac et al. 2005).
The main result of these studies is to show the very crucial role played by the membrane constitutive law when the capsule is subjected to large deformations: a capsule with a strain hardening law (e.g. SK law) can sustain larger shear rates without breaking than a capsule with a strain softening membrane (e.g. MR law).
There are very few studies of the hydrodynamic interactions between capsules. We have considered the simple case where two identical pre-inflated capsules interact in a simple shear flow. The model shows that during crossing the elastic tension level in the membrane increases. During separation, buckling may occur when the curvature of the film between the two capsules changes sign. Furthermore the distance between the two capsules increases after deformation and this phenomenon should lead to finite self-diffusion and non-newtonian effects in a semi dilute suspension of identical capsules (Lac et al. 2007, 2008).

The arrows show the direction of motion of each capsule. Time increases from (a) to (d).
The color code shows the normal load on the membrane (decreasing load from red to blue)
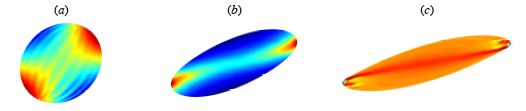
The large deformations of an initially-ellipsoidal capsule in a simple shear flow are studied by coupling a boundary integral method for the internal and external flows and a finite element method for the capsule wall motion. Oblate and prolate spheroids are considered (initial aspect ratios: 0.5 and 2) in the case where the internal and external fluids have the same viscosity and the revolution axis of the initial spheroid lies in the shear plane. Two regimes are found depending on the value of a capillary number comparing viscous and elastic forces. At low capillary number, the capsule tumbles, behaving mostly like a solid particle. At higher capillary numbers, the capsule has a fluid-like behaviour and oscillates in the shear flow while its membrane continuously rotates around its deformed shape. During the tumbling-to-swinging transition, the capsule transits through an almost circular profile in the shear plane for which a long axis can no longer be defined. The critical transition capillary number is found to depend mainly on the initial shape of the capsule and on its shear modulus, and weakly on the area-dilatation modulus. Qualitatively, oblate and prolate capsules are found to behave similarly, particularly at large capillary numbers when the influence of the initial state fades out. However, the capillary number at which the transition occurs is significantly lower for oblate spheroids.

Prolate ellipsoidal capsule in a simple shear flow over one half period
The dot is a material point of the membrane and the coor code represents the normal load.
(a) Low shear tumbling regime; (b) transition regime; (c) swinging regime
There are many situations where a capsule is forced to flow through a pore (filtration, microciculation, microfluidics)
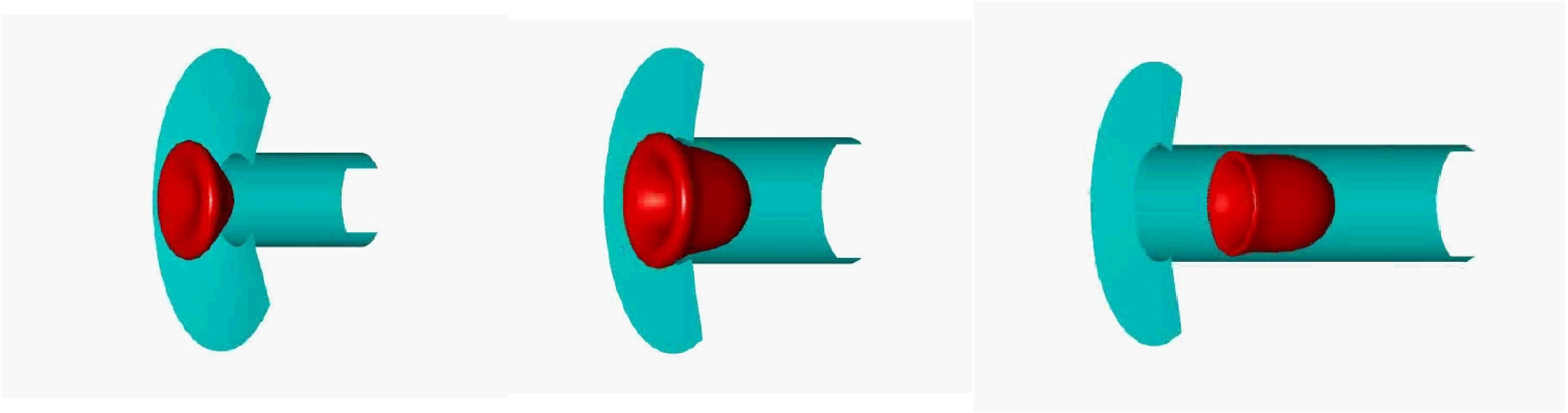
The entrance into the pore is a transient process that depends on
Once the capsule has reached a steady shape inside the tube, the membrane is at rest and the internal viscosity has no effect.
For initially spherical capsules, pre-inflation due to osmotic
effects
may also have an important role (Lefebvre & Barthes-Biesel
2007). A comparison with the model and
experimental observations of capsules with alginate membranes flowing
in a cylindrical tube (Risso et al. J. Fluid Mech. 2006) shows that the
experimental capsules were indeed subjected to a small pre-inflation
and that their membranes seem to obey the SK law.
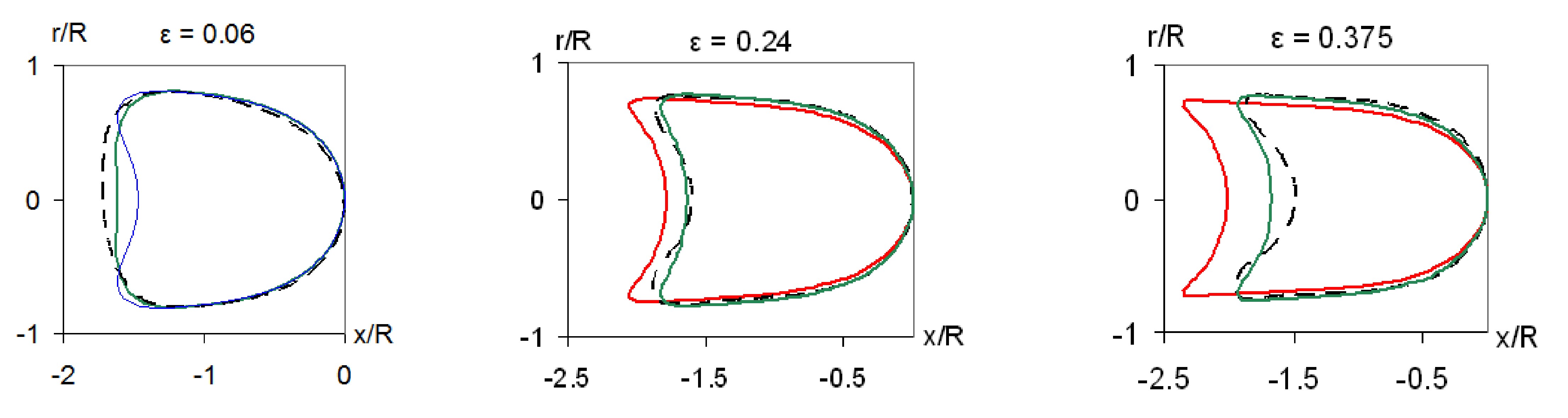
dashed line: experiment (Risso et al. J. Fluid Mech. 2006); blue: SK law, no pre-inflation; green: SK law with 3% pre-inflation; red: ES law with 3% pre-inflation.
This numerical model can also be used to analyze the flow of artificial micro-capsules in micro pores and to deduce a value of the membrane shear elastic modulus (see determination of membrane properties)