|
Avertissement
|
Si vous arrivez directement sur
cette page, sachez que ce travail est un rapport d'étudiants et doit
être pris comme tel. Il peut donc comporter des imperfections ou des
imprécisions que le lecteur doit admettre et donc supporter. Il a été
réalisé pendant la période de formation et constitue avant-tout un
travail de compilation bibliographique, d'initiation et d'analyse sur
des thématiques associées aux technologies biomédicales. Nous ne faisons aucun usage commercial et la
duplication est libre. Si vous avez des raisons de contester ce droit
d'usage, merci de nous en faire part .
L'objectif de la présentation sur le Web est de permettre
l'accès à l'information et d'augmenter ainsi les échanges
professionnels. En cas d'usage du document, n'oubliez pas de le citer
comme source bibliographique. Bonne lecture...
|
|
Les calculs de capabilité dans la production
industrielle
|
|
|
|
|
|
|
|
RESUME
Les entreprises évolues, depuis quelques
décennies maintenant, dans une atmosphère de compétitivité
accrue. La Maitrise
Statistique des Procédés (MSP) répond à un passage d'une stratégie de contrôle à une stratégie de
prévention. Mais que recouvre cette méthode, et quels en
sont les fondements ? A
travers notre étude nous développerons un des deux outils de la MSP,
les
calculs de capabilité, en s'appuyant sur des normes qui
définissent différentes méthodes de calculs de capabilité, et sur des
études de cas pour réaliser l'ampleur de cet outil.
Mots clés: capabilité, indicateur, centrer,
dispersion, intervalle de
tolérance
|
ABSTRACT
The companies evolve,
since some decades now, in an atmosphere of increased competitiveness.
Statistic Process Control (SPC) answers a passage of a strategy
of control to a strategy of prevention. But what covers this method,
and which are the bases? Through our study we will develop one of the
two tools of the SPC, calculations of capability, while being based on
standards which define various methods of calculation from capability,
and on case studies to carry out the width of this tool.
Keywords: capability, indicator, centre, dispersion,
interval of tolerance,
|
Remerciements
Nous
remercions, Mr Jean-Pierre Caliste notre tuteur de projet ainsi que Mr
Gilbert
Farges pour leurs conseils, leurs aides et le temps qu’il nous ont
consacré
tout au long du projet
Sommaire
Introduction
I Role
de la MSP
1 Historique
2 Loi
Normale
3
Présentation
des indicateurs
II Calcul
de capabilité
1 Tableau
des normes
2 Approche CNOMO
3 Approche QS9000
4 Tableau récapitulatif
III Etude de cas
1 La scie automatique
2 Arbre Palier
3 Exemple de déploiement
Bilan
Conclusion
Bibliographie
Dans un monde de plus en plus
réactif, il faut savoir se démarquer très vite de ses concurrents. La
qualité est donc un point clé de la compétitivité, on doit être capable
de répondre rapidement aux exigences du client. Mais comment la MSP (Maitrise Statistique des Processus)
contribue-t-elle à assurer une qualité optimum par une utilisation de
l’outil statistique ? A travers cette synthèse nous étudierons la
MSP, son rôle et son impact ensuite nous présenterons les différents
calculs de capabilité, puis nous exposerons deux applications suivies
d’un bilan.
Il faut ajouter que cette étude a
été menée dans le souci d’apporter une approche claire et succincte,
pour des néophytes.
I.Role de la
MSP
Shewhart
a présenté en 1929 sa célèbre « Control Chart
(carte de controle) » dans l’industrie militaire, ouvrant ainsi la voie
à une nouvelle discipline qu’est la M.S.P.
Tout d’abord oubliée, ce n’est que dans les années 60 que Deming a su insuffler un regain d’intérêt à
cette technique en l’appliquant dans l’industrie Japonaise. Ensuite
dans les années 70 on voit apparaître les calculs de capabilité dans
l’industrie automobile Américaine et c’est seulement dans les années 80
que cette discipline s’est imposée en Europe.
Cependant
de nombreuses évolutions dans la Maîtrise Statistique des Procédés
(MSP) sont apparues ces dernières années.
Ces évolutions sont de trois
ordres : conceptuelles,
méthodologiques et normatives :
- Les évolutions conceptuelles concernent
principalement la notion de conformité. La conformité du produit qui
était largement fondée sur le simple respect des tolérances est plus
liée désormais au centrage sur la cible.
- Les évolutions méthodologiques concernent
tous les aspects de la MSP, avec l’application de nouvelles cartes de
contrôle, les évolutions sur les calculs des capabilités (aptitudes) et
l’application de la MSP dans les cas spéciaux.
- Les évolutions normatives sont également
importantes avec l’apparition de nouvelle normes sur le sujet tant au
niveau de l’AFNOR qu’au niveau de l’ISO.
La
MSP, qui s'inscrit dans une stratégie de prévention et dont l’objectif
est d'améliorer la qualité d'une production, a donc connu un fort
développement dans l'industrie européenne ces vingt dernières années.
Cette outil nous permet de diminuer les dérives,
d’augmenter la performance du processus, mais aussi de baisser les couts de non qualité. C’est un outil de pilotage
des machines qui nous assure une meilleure qualité des produits et une
fiabilité optimum du fonctionnement du processus.
Il
existe deux concepts essentiels composant la M.S.P
:
- Suivi et pilotage des procédés par cartes de
contrôle :
-Echantillonnage
-Pilotage
des procédés par cartes de contrôle
-Interprétation
des cartes de contrôle
-Gestion
de traçabilité : journal de bord
-Capabilité
machine
-Capabilité
procédé
Bien
que les concepts de capabilité et de carte de contrôle n’aient pas été
introduits en même temps, ils sont très étroitement liés. De plus dans
la suite de notre synthèse nous développerons plus précisément le
calcul de capabilité.
Les calculs de capabilité
présentés ici sont basés sur l’hypothèse que le procédé visé obéisse à
une loi normale (loi de Gauss). S’il en est différemment, les calculs
et interprétations ci-dessous n’ont plus de sens.
3.
Présentation des
indicateurs
Avant de rentrer dans les calculs,
le terme « capabilité » est à définir
Capabilité
: Aptitude du processus à satisfaire les spécifications du client.
Il faut savoir qu’il existe deux types d’indicateurs de
capabilité : la dispersion et le centrage
On retrouve cet indicateur sous la
forme suivante :
Indice
de capabilité (dispersion) :
Intervalle
de tolérance
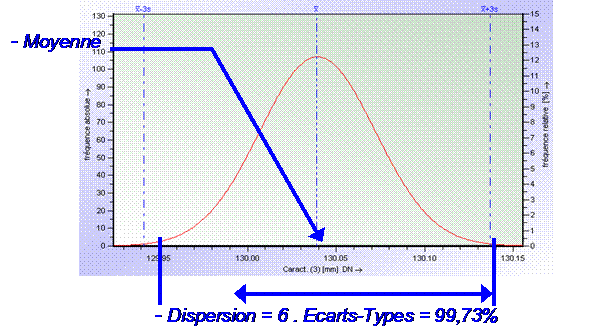
Dispersion = 6 * sigma
Dispersion
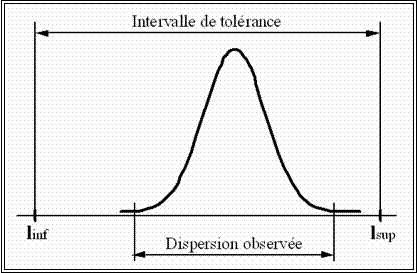
Intervalle
de tolérance = Limite supérieure (LTS) - Limite inférieure (LTI)
Indice
de capabilité (centrage) : (distance
entre la moyenne et la limite la plus proche)/3*sigma
En d’autre
terme à : min [(LTS – Xbar)/3*sigma ;
(Xbar – LTI)/3*sigma)
Il faut ensuite différencier les
capabilités court terme et long terme, on parlera de court terme
(capabilité machine) lorsqu’on observe la dispersion instantanée qui
généralement est causé par le moyen de production. Puis le long terme
(capabilité procédé) est traduit par une dispersion globale, cette
dispersion a comme origine les variations liées aux 5M (Moyen,
Milieu, Main d’œuvre, Matière, Méthodes).
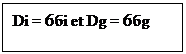
Capabilité court terme (Cm) : Intervalle de tolérance/Dispersion instantanée
(Di)
Capabilité
court terme (Cp) : Intervalle de tolérance/Dispersion globale (Dg)
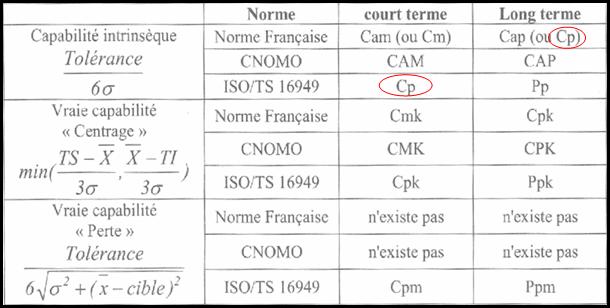
Il est aussi important de rajouter
que selon les normes on retrouvera des notations différentes, donc il
faut être vigilant quand on utilise ces notations et toujours indiquer
les références. Voici ci-dessous un tableau récapitulatif regroupant
nos différentes normes liées au calcul de capabilité où on retrouve les
indicateurs :
La
première étape est le prélèvement des valeurs, mais il n’est pas à
effectuer sans prendre quelques précautions. La production doit être en
accord avec les configurations du cahier des charges, et les moyens de
mesures doivent être capable. Pour l’exemple, nous prendrons la loi
normale comme modèle statistique, il est donc nécessaire de faire un
prélèvement d’au moins 30 pièces sans modifications pendant le
prélèvement. Une fois les prélèvements effectués, il est important
d’effectuer une vérification de la normalité de l’échantillon.
Pour ce faire, on détermine le nombre de
classe selon la formule : Kt
= 1 +[10 lg
(N)/3] L 'étendue de mesure [Wt
= (écart max. - écart min.)] permet de
calculer l'intervalle de classe Ht =Wt/Kt. L'intervalle
de classe théorique doit être arrondie au nombre supérieur compatible
avec la résolution de la mesure. On test la normalité grâce au test de
Khi 2, ou grâce, une fois tracée, à la doite de Henry.
Pour
calculer la moyenn MX, on a la formule : Mx
= (somme de 1 à N des Xi)/N
Pour
calculer l'écart type S de l'échantillon, on a la formule : S= Racine de [(somme de 1 à N de (Xi-Mx)²)/(N-1)]
La
capabilité moyen qui mesure globalement la
faculté du moyen à tenir la tolérance, est quantifiée par le
Coefficient d'Aptitude des Moyens (CAM).
CAM
= IT/D
IT
: intervalle de tolérance
D =
6.Si : Dispersion machine
CAP=IT/Dg=IT/6.Sg Sg=C.S
C est défini dans le tableau ci dessus, suivant le nombre de pièces N.
|
N
|
10
|
12
|
16
|
20
|
24
|
28
|
30
|
35
|
40
|
50
|
75
|
100
|
|
C
|
1,64
|
1,55
|
1,43
|
1,37
|
1,32
|
1,30
|
1,28
|
1,26
|
1,24
|
1,21
|
1,16
|
1,13
|
En cas de dérèglement maxi :
Cpk=(LTS-Mx)/(3.C.S)
En cas de dérèglement mini :
Cpk=(Mx-LTI)/(3.C.S)
Dans la CNOMO, un procédé est
capable si Cpk>1
Si = C.Sb/C4
ou Si = C.Rb/d2
pour C4 et d2 voir table
|
n
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
d2
|
1.128
|
1.693
|
2.059
|
2.326
|
2.534
|
2.704
|
2.847
|
2.970
|
3.078
|
3.173
|
3.258
|
|
c4
|
0.7919
|
0.8862
|
0.9213
|
0.940
|
0.9515
|
0.9594
|
0.9650
|
0.9693
|
0.9727
|
0.9754
|
0.9776
|
Suivant les
valeurs de Cam ou Cmk, on classe
généralement la capabilité comme :
C <
0.67
Très mauvaise
0.67 < C
< 1
Mauvaise
1 < C
< 1.33
Très moyenne
1.33 < C
< 1.67 Moyenne
1.67 < C
< 2
Bonne
C > 2
Très bonne
Le procédé
est dit capable si le Cpk est supérieur à
1 : on accepte que 3 pièces sur 1000 soient hors tolérance.
Si le procédé n'est pas considéré
capable, alors il est nécessaire d'entreprendre une amélioration du
procédé.
Le référentiel QS9000 à été créé
en 1994 par les constructeurs américains (Ford, Général Motors et Chrysler), pour améliorer le système
qualité des entreprises, diminuer les gaspillages et renforcer
l’amélioration continue. Il a été élaboré sur la base de l'ISO 9001, additionné de spécifications propres
au secteur automobile.
Le QS-9000 est
accompagné de 6 manuels:
• QSA - Quality system Assessment
• PPAP - Production Part Approval Process
• APQP - Advanced Product Quality Planning and Control Plan
• FMEA - Failure Mode Effect and Analysis
• MSA - Measurement System Analysis
• SPC - Statistical Process Control
Nous nous intéresserons plus particulièrement au
manuel SPC pour aborder les indicateurs de capabilité.
A travers
ce référentiel il existe deux types d’indicateurs (voir le tableau des
normes - figure x ) :
à Court
terme (Cp, Cpk)
à Long
terme (Pp, Ppk)
Ensuite on
estime l’écart type instantané : Si = C.Sb/C4
ou Si = C.Rb/d2
Les
coefficients c4 et d2 sont donnés en fonction de la taille de
l’échantillon (annexe 1)
Voici
ci-dessous les indicateurs courts termes :
Cp
=
IT/6.Si
Cpk = min [(LTS – Xbar)/3.Si ;
(Xbar – LTI)/3.Si]
De même,
on estime l’écart type global : Sg= Racine de [(somme de 1 à N de (Xi-Xbar)²)/(N-1)]
Voici
ci-dessous les indicateurs longs termes :
Pp
=
IT/6.Sg
Ppk = min [(LTS – Xbar)/3.Sg ;
(Xbar – LTI)/3.Sg]
Il est important de noter que les
indicateurs les plus importants sont le Pp et le Ppk
car ils traduisent la qualité des pièces livrées au client.
Le procédé est capable sur le long
terme lorsque Ppk > 1,33 et Pp le plus
proche possible,
aussi il faut avoir Cpk > 1,33 et Cp
>Cpk >1,33 sur le court terme.
Annexe 1
Tableau de
coefficients
|
ESTIMATION DE L’ECART TYPE
|
|
N
|
C4
|
D2
|
|
2
|
0,7979
|
1,128
|
|
3
|
0,8862
|
1,693
|
|
4
|
0,9213
|
2,059
|
|
5
|
0,9400
|
2,326
|
|
6
|
0,9515
|
2,534
|
|
7
|
0,9594
|
2,704
|
|
8
|
0,9650
|
2,847
|
|
9
|
0,9693
|
2,970
|
|
10
|
0,9727
|
3,078
|
|
11
|
0,9754
|
3,173
|
|
12
|
0,9776
|
3,258
|
|
13
|
0,9794
|
3,336
|
|
14
|
0,9810
|
3,407
|
|
15
|
0,9823
|
3,472
|
|
20
|
0,9869
|
3,735
|
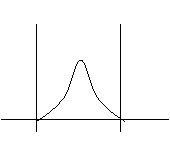
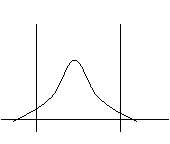
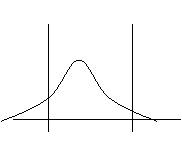
Ce tableau est un moyen visuel
pour situer l’état de notre processus et de caractériser ainsi l’écart
entre la situation réelle et notre objectif.
Le graphe de référence se trouve
au centre du tableau, et les variations sont représentées par rapport à
ce graphe.
|
Cam augmente
|
Cam constant
|
Cam diminue
|
|
Cmk
augmente
|
 1 1
|
2
|
3
|
|
Cmk
constant
|
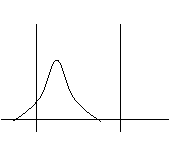 4 4
|
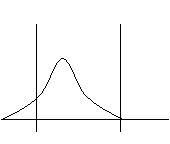
5
|

6
|
|
Cmk
diminue
|
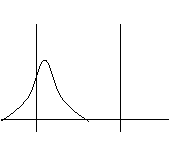 7 7
|
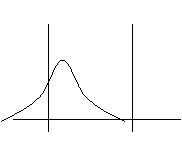
8
|
9
|
De la situation 5 à 1 : - Le centrage et la
dispersion se sont
améliorés, c'est le cas idéal
De la
situation 5 à 2 : - Le centrage a été amélioré mais la dispersion
n'a pas évoluée
De la
situation 5 à 3 : - Le centrage s'est amélioré mais la dispersion
s'est dégradée
De la
situation 5 à 4 : - La dispersion s'est améliorée et le centrage
reste le même
De la
situation 5 à 6 : - Le centrage ne change pas par contre la
dispersion augmente
De la
situation 5 à 7 : - Le centrage s'est dégradé mais la dispersion
est meilleure
De la
situation 5 à 8 : - La dispersion reste la même et le centrage se
dégrade
De la
situation 5 à 9 : - Il y a une dégradation de la dispersion et du
centrage
Pour que le lecteur comprenne ce
raisonnement, il est utile de présenter des applications. Dans un
premiers temps nous présenterons un exercice que nous avons imaginé,
c’est l’exemple d’une scie automatique ou on étudiera son aptitude à
produire des pièces conforme aux spécifications clients. Puis dans un
second temps nous reprendrons un cas fréquent en MSP, l’arbre-palier.
On imagine un processus de
fabrication, mécanique qui usine des cales de précision, il est alors
utile de maitriser ce processus.
Voici des schémas ci-dessous :

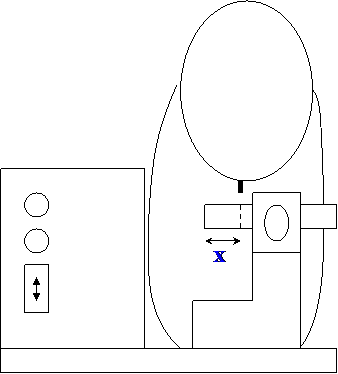
On considère la cale acceptable
lorsque X : 5,5 + ou – 0,04 cm, aussi il est important de préciser
que cette étude s’effectuera selon le référentiel QS9000.
Des mesures
ont été effectuées sur un échantillon de 30 pièces consécutives, voici
les résultats :
|
Piece
|
Cale
(X en cm)
|
Piece
|
Cale
(X en cm)
|
Piece
|
Cale
(X en cm)
|
|
1
|
5,509
|
11
|
5,495
|
21
|
5,493
|
|
2
|
5,519
|
12
|
5,472
|
22
|
5,513
|
|
3
|
5,464
|
13
|
5,509
|
23
|
5,504
|
|
4
|
5,528
|
14
|
5,486
|
24
|
5,499
|
|
5
|
5,477
|
15
|
5,516
|
25
|
5,508
|
|
6
|
5,532
|
16
|
5,493
|
26
|
5,509
|
|
7
|
5,499
|
17
|
5,511
|
27
|
5,499
|
|
8
|
5,481
|
18
|
5,502
|
28
|
5,485
|
|
9
|
5,512
|
19
|
5,489
|
29
|
5,497
|
|
10
|
5,526
|
20
|
5,485
|
30
|
5,504
|
Selon le
référentiel QS9000 :
A)
Estimer l’écart type instantané ? En
déduire la dispersion Di.
B)
Calculer les indicateurs Cp et Cpk.
C)
Vérifier la normalité.
D)
Est-ce que le processus est capable ?
E)
On remarque dans ce process un taux élevé de
rebuts, quelles améliorations pouvez-vous apporter ?
A)
Tout d’abord on calcule l’intervalle de
tolérance, ainsi que la moyenne et l’écart type. La dispersion étant
égale à 6 fois l’écart type.
IT = LTS –
LTI = 5,54 – 5,46 = 0,08.
|
Moyenne
|
5,50053333
|
|
Ecart type
|
0,01633852
|
|
Dispersion
|
0,0980311
|
B)
Ensuite on calcule les indicateurs de capabilité
Cp et Cpk.
|
IT
|
0,08
|
|
Cp
|
0,816067555
|
|
Cpk
|
0,805186654
|
C)
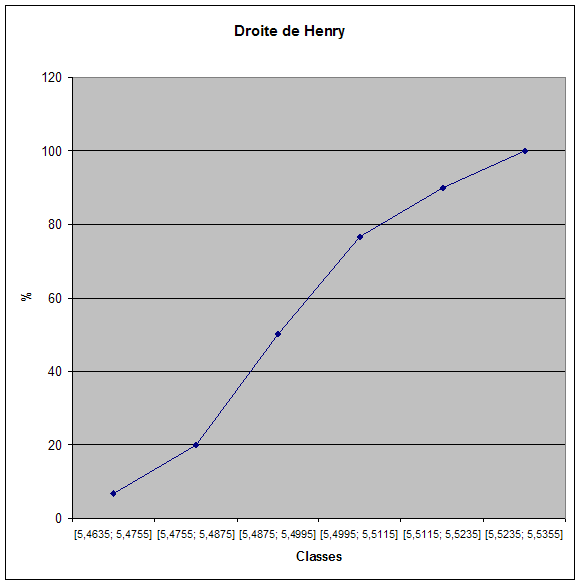
Pour vérifier si cette étude suit la loi
normale, nous utiliserons la droite de Henry. Pour ce faire il nous
faut calculer le nombre de classe KT.
KT = 1
+ 10 log 30 = 6
3
Puis on calcule l’intervalle de
classe Ht = Wt
/ KT et Wt = (max – min) =
(5,532 – 5,464) = 0,068
Ht =
0,068 / 6 = 0,012 puisqu’il faut arrondir au supérieur.
Alors on a 6 classes avec comme
intervalle 0,012 et il nous suffit de faire le cumulé pour tracé notre
droite de Henry.
|
KT=6
|
6
classes
|
|
Ht
= 0,012
|
|
|
Classe
|
|
Cumulé
|
%
|
|
[5,4635;
5,4755]
|
2
|
2
|
6,66666667
|
|
[5,4755;
5,4875]
|
4
|
6
|
20
|
|
[5,4875;
5,4995]
|
9
|
15
|
50
|
|
[5,4995;
5,5115]
|
8
|
23
|
76,6666667
|
|
[5,5115;
5,5235]
|
4
|
27
|
90
|
|
[5,5235;
5,5355]
|
3
|
30
|
100
|
On remarque
que les points sont alignés, l’hypothèse de la loi normale est vérifiée.
D) Le
process n’est pas capable puisque Cp et Cpk
sont inférieurs à 1,33, les mesures à prendre sont donc une révision
des spécifications clients pour ne pas faire de surqualité mais avant
cela régler la machine.
E)
Les améliorations à apporter sont : une
bonne lubrification, un guidage de la lame, un bon nettoyage, une bonne
maintenance et un meilleur maintien de notre cale.
Soit un
arbre et un palier définis par les spécifications et les schémas
suivants :
Les
spécifications client sont :
"� Pour le
diamètre de l’arbre X : 3.250 ± 0.025 cm
"� Pour le
diamètre du palier Y : 3.270 ± 0.030 cm
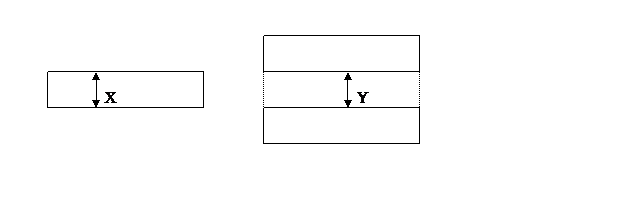
Dans la
fabrication de l’arbre et du palier en grande série, nous avons relevés
les 30 valeurs du tableau ci-dessus (en centimètres). Cet échantillon
suit une loi normale.
|
Prélèvement
|
Arbre
X (cm)
|
Palier
|
Prélèvement
|
Arbre
|
Palier
|
|
1
|
3,264
|
3,25
|
16
|
3,263
|
3,25
|
|
2
|
3,265
|
3,248
|
17
|
3,266
|
3,251
|
|
3
|
3,26
|
3,249
|
18
|
3,266
|
3,249
|
|
4
|
3,266
|
3,249
|
19
|
3,263
|
3,249
|
|
5
|
3,254
|
3,251
|
20
|
3,256
|
3,25
|
|
6
|
3,267
|
3,252
|
21
|
3,256
|
3,251
|
|
7
|
3,262
|
3,251
|
22
|
3,264
|
3,252
|
|
8
|
3,256
|
3,249
|
23
|
3,26
|
3,251
|
|
9
|
3,258
|
3,25
|
24
|
3,265
|
3,251
|
|
10
|
3,263
|
3,25
|
25
|
3,257
|
3,25
|
|
11
|
3,263
|
3,249
|
26
|
3,264
|
3,25
|
|
12
|
3,258
|
3,25
|
27
|
3,265
|
3,249
|
|
13
|
3,261
|
3,25
|
28
|
3,264
|
3,25
|
|
14
|
3,268
|
3,249
|
29
|
3,258
|
3,25
|
|
15
|
3,261
|
3,249
|
30
|
3,261
|
3,25
|
A partir de
ces valeurs, nous pouvons calculer les variables suivantes :
|
Variable
|
Arbre
|
Palier
|
|
Moyenne
|
3,2618
|
3,25
|
|
Ecart
type
|
0,0038
|
0,001
|
|
Di
|
0,0226
|
0,0058
|
|
IT
|
0,05
|
0,06
|
|
Cam
|
2,2141
|
10,37
|
|
Cmk
|
1,1691
|
3,4452
|
Les
résultats sont probants, la dispersion est bonne (supérieure à 2) pour
les deux éléments, le centrage pour l’arbre n’est pas satisfaisant mais
permet à l’échantillon de rester dans l’IT,
et le centrage du palier est excellent car supérieur à 2.
Il peut
être intéressant de se pencher sur le rendu graphique des résultats.
Graphique des résultats
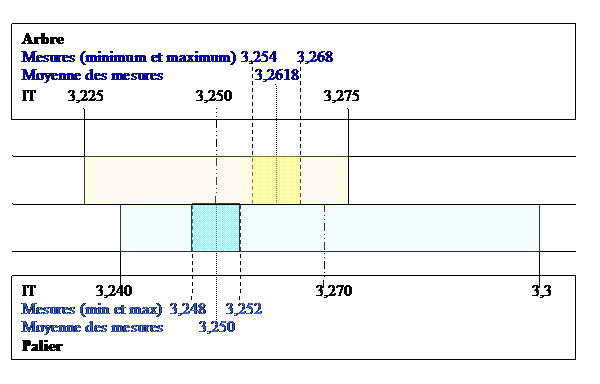
Cet exemple
soulève le problème de l’adéquation des capabilités entre elles, car il
est évident que tous les arbres ont un diamètre supérieur aux diamètres
des paliers. Ici il serait important de recentrer les deux processus,
même si le centrage du palier est bon et que celui de l’arbre lui
permet de rester dans l’IT.
Nous avons recueillie le témoignage d’un
constructeur mondial durant notre étude, nos questions se sont portées essentiellement
sur l’utilisation de cet outil au sein d’une entreprise. L'aspect " politique
" a été présenté, avec la puissance de cet outil et ces limites.
Les indicateurs de capabilité sont
un bon moyen de sélectionner les fournisseurs et de se mettre d’accord
sur la qualité d’un produit. Autrefois il y avait des malentendus avec
les fournisseurs, car les exigences des constructeurs étaient perçu
comme étant des exigences minimales, et cette écart se caractérisé soit
par de la sur qualité soit par un mauvais travail. Aujourd’hui les
indicateurs nous permettent de fixer des critères mesurables, le
constructeur optimise ces couts et le
fournisseur possède un objectif concret. En effet ces indicateurs sont
un bon outil de négociation, ils permettent ainsi une bonne entente
entre constructeurs et fournisseurs en visant une qualité du produit
respectant les spécifications client.
En général les indicateurs à court
terme sont mise en œuvre assez facilement puisqu’il suffit de prélever
30 pièces, la seule variabilité étant celle de la machine. Par contre
les indicateurs à long terme traduisent d’une variabilité des 5M
(Moyen, Méthode, Mesure, Matière, Main d’œuvre) et le discours de ce
grand constructeur souligne la difficulté de mettre en œuvre ces
indicateurs. En effet le facteur le plus variable étant le milieu, on
imagine bien que la température d’un atelier est un facteur difficile à
faire varier.
Nous sommes dans un contexte de
forte concurrence où les exigences des clients deviennent de plus en
plus précises, il faut savoir répondre très rapidement à ces attentes
pour gagner de nouveaux marchés. La MSP nous permet ainsi de maîtriser
notre production en livrant des produits conformes aux spécifications
des clients. Son but étant la détection des dérives d’un process grâce
aux cartes de contrôle et sa correction par l’établissement de plan
d’actions. Toutefois il faut surveiller l’évolution de notre process
avec des calculs de capabilité. A travers cette synthèse où sont
exposées les différentes approches de calculs, il est primordial de
souligner que la priorité de ces indicateurs est la prévention des
dérives pour tendre vers le zéro défauts.
La MSP est un outil indispensable,
très utilisé dans les grandes entreprises, en utilisant l’outil
statistique la MSP a su apporter un peu plus de rigueur dans les
méthodes et l’organisation. Il est sûr que cet outil se déploiera de
plus en plus dans le futur dans toutes les entreprises.
Cette synthèse traduit
l’importance et l’impact des indicateurs de capabilité en entreprise,
tout au long de notre étude nous avons abordés les calculs de
capabilité selon différentes approches. Cela nous permettra
d’approfondir nos notions en MSP, en resituant les différentes normes à
l’aide des études de cas.
Il faut noter que cette étude
traite la majorité des cas hormis les petites séries (échantillon <
30 pièces) et les situations qui ne suivent pas une loi normale. Cette
étude est alors utilisable pour une première approche mais nécessite un
management MSP global pour la mise en place.
Sites
Internet :
http://www.cyber.uhp-nancy.fr/
http://www.cyber.uhp-nancy.fr/
http://www.abwconcept.com/
Cours
:
Les
outils pour la MSP de Mr BOUDAOUD, filière FQI, UTC
Maîtrise
statistique des processus ENSGI 2A, INP Grenoble
Ouvrages :
La
qualité : démarche, méthodes et outils sous la direction
de Madame Zohra CHERFI, filière FQI
Hermès science publications ISBN : 2-7462-0425-8
Appliquer
la maîtrise statistique des procédés MSP/SPC
M. Maurice PILLET Édition
d’organisation ISBN : 2-7081-2672-5
Thèses :
Maurice
Pillet - 11/06/93 - "Les Outils statistique dans l'approche qualité
totale"
Emmanuel
Duclos - 27/11/97 - "Contribution à la maitrise statistique des
procédés - Cas des procédés non normaux "
retour
sommaire


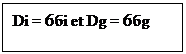

 1
1 

 4
4 
 7
7