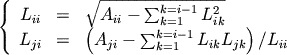On montre que A, matrice NxN
inversible quelconque, peut être décomposée
sous la forme :
Si en plus d'être définie,
c'est
à dire inversible, la matrice A est positive, alors
la décomposition précédente est telle que l'on
peut choisir :
.
La résolution du système
linéaire :
,
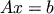b étant un vecteur connu (second membre) de dimension N et x étant un vecteur inconnu de dimension N, revient donc à la résolution successive des deux systèmes triangulaires suivant :
,b étant un vecteur connu (second membre) de dimension N et x étant un vecteur inconnu de dimension N, revient donc à la résolution successive des deux systèmes triangulaires suivant :
puis 
Cette méthode est un cas particulier de
la décomposition LU. Son avantage est la réduction
significative des coûts de calculs :
opérations contre
avec la méthode de Gauss.
De plus, si l'on ajoute la condition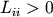 
, alors
la matrice L est unique telle que :
, alors
la matrice L est unique telle que :
