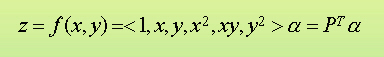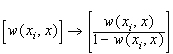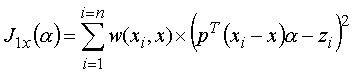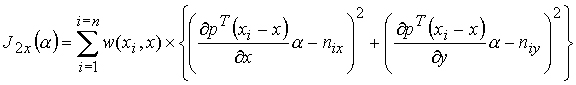|
 |
Pag e précédente |
|
|
| Page précédente |
|
|
|
|
|
Principe
Nous souhaitons d'une part déterminer localement une équation de surface pour positionner les nœuds du maillage raffiné sur la surface interpolée et contrôler le processus de "déraffinement" et d'autre part calculer en tout point les courbures afin de les relier à un estimateur d'erreur sur la géométrie dans un simple souci de ne pas dégrader le modèle géométrique.
|
|
|
Le calcul des courbures principales d'une surface nécessite un paramétrage. Nous supposons qu'en chaque nœud de la surface discrétisée, il existe un voisinage sur lequel la surface peut être définie localement dans un repère orthonormal direct par une surface de Monge d'équation cartésienne z=f(x,y) où f désigne une fonction numérique de classe C2 sur un domaine plan.
On cherche l'équation sous la forme d'une quadrique qui s'exprime dans le système de coordonnées locales par
où a est un vecteur de 6 coefficients à déterminer.
Haut de page
|
|
|
|
|
|
|
|
|
|
|
Construction d'un modèle géométrique local
Haut de page
Au cours du processus d'adaptation de maillage, de nouveaux nœuds sont créés sur le modèle géométrique. De nombreuses requêtes sur le maillage initial sont alors effectuées afin de déterminer "la surface" sur laquelle on souhaite projeter le point. En premier lieu, il faut rappeler que le choix du support d'interpolation (un ensemble de points) dans une méthode de moindres carrés mobiles dépend de la position du point où l'on souhaite réaliser l'évaluation. De même, les coefficients de la surface varient de façon continue au fur et à mesure que l'on se déplace sur le maillage initial. En pratique et notamment dans le cadre de notre application de remaillage de surface, l'expérience montre que les opérations de projection d'un point sur un maillage peuvent s'accompagner d'erreurs numériques dues à l'ambiguïté de certaines configurations. La méthode que nous avons proposée permet de résoudre complètement les problèmes de projection sur un maillage. Les méthodes sans maillage apportent une solution souple, efficace et très robuste à ce genre de problème.
En pratique, le point que l'on souhaite positionner sur la géométrie reconstruite est le centre d'une arête du maillage. Le paramétrage de la surface de Monge d'équation cartésienne z=f(x,y) est défini dans un repère orthonormal direct. Plusieurs méthodes ont été proposées pour la détermination du repére local associé à la forme quadratique de la surface. Sans entrer dans les détails, il est en effet possible :
· de choisir un repère lié à la face la plus proche,
· de déterminer un repère au sens des moindres carrés en utilisant un support d'interpolation basé sur une recherche de plus proches voisins,
· enfin, d'utiliser l'approximation diffuse pour déterminer un plan dont les paramètres varient continûment au cours du déplacement du point sur le modèle. Cette approche permet d'éliminer les problèmes de projection.
Fonctions Poids
Toutes les grandeurs référencées par la suite sont exprimées dans le système de coordonnées locales. Pour chaque point d'évaluation x du plan de projection, on ne retient que les nœuds xi les plus proches. L'influence du nœud xi est réglée par les fonctions poids wi. Les fonctions poids sont des fonctions radiales qui décroissent avec la distance au point d'évaluation ainsi que le montre la Figure suivante. Notons qu'il faut au moins 6 points pour déterminer les coefficients.
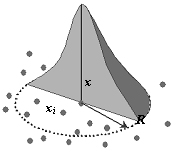
Fonction poids
Haut de page
Dans la pratique, une fonction cubique a été choisie. Celle ci s'annule à l'extérieur du domaine d'influence. Le domaine d'influence est centré au point d'évaluation et on fait l'hypothèse que tous les nœuds participant à l'interpolation sont dans un cercle de rayon R (Figure suivante).
Les fonctions poids sont données par :
di désigne la distance du nœud xi au point d'évaluation calculée dans le plan de projection
Par ailleurs, dans sa version habituelle, l'approximation diffuse n’est pas interpolante. Les poids ont été remplacés par des poids interpolants par la substitution (interpolation de Shepard).
On peut remarquer que dans sa version interpolante, les fonctions d'interpolation forme une partition de l'unité.
Support d'interpolation

Support d'interpolation
Haut de page
Résolution
L'interpolation Diffuse de type Hermite s'écrit sous la forme de deux critères.
Le premier critère traduit l'interpolation aux nœuds et s’exprime par
Le second critère exprime la colinéarité entre la normale calculée ou donnée par le modèle géométrique réel (le maillage par exemple) et la normale à la surface diffuse et sexprime sous la forme
Les coefficients de la surface sont obtenus en minimisant la somme pondérée des 2 critères.
Le calcul de la normale ne prend pas en compte les variations de a et on ne dérive que la partie polynomiale. Ceci revient à reprendre la notion de "dérivée diffuse" introduite par Nayroles et al. [117].