Les algorithmes quantiques
Algorithme de Deutsch
Histoire
L’algorithme de Deutsch est l’un des algorithmes quantiques les plus connus. Découvert en 1985 par David Deutsch, physicien israélo-britannique, il fut le premier exemple montrant qu’un ordinateur quantique pouvait être plus performant qu’un ordinateur classique. L’algorithme de Deutsch n’a pas vraiment d’utilité, mais sa simplicité permet de bien comprendre les bases de l’algorithmie quantique. Il est généralement le premier algorithme quantique enseigné à des nouveaux élèves.
Enoncé du problème
Etant donné une fonction booléenne $ f:\{0,1\} \rightarrow \{0,1\} $. Il en existe 4:
| x | f(x) |
|---|---|
| 0 | 0 |
| 1 | 0 |
FONCTION CLEAR
| x | f(x) |
|---|---|
| 0 | 1 |
| 1 | 1 |
FONCTION SET
| x | f(x) |
|---|---|
| 0 | 1 |
| 1 | 0 |
FONCTION NOT
| x | f(x) |
|---|---|
| 0 | 0 |
| 1 | 1 |
FONCTION ID
Cette fonction nous est donnée sous la forme d’un oracle (aussi appelé boîte noire), qui à partir des entrées produit une sortie, sans que l’on connaisse le mécanisme à l’intérieur. On sait qu’un tel oracle est physiquement réalisable puisque la porte de Toffoli permet de réaliser toute fonction classique de manière réversible. L’algorithme de Deutsch permet de résoudre la question suivante : comment savoir si la fonction est constante ou non ?
La porte $ U_f $
L’algorithme de Deutsch introduit une porte quantique particulière à 2 qubits appelée $ U_f $. Elle est définie comme suit :
\(U_f\ket{x,y} = \ket{x, y \oplus f(x)}\)
Cette porte permet d’appliquer la fonction \(f\) au qubit \(x\). On appelera les qubits d’entrées de la fonction (ici $ x $) le registre de donnée et le qubit de sortie le registre cible. Cette porte est réversible et unitaire et est la porte standard utilisée dans les algorithmes quantiques pour appliquer une fonction à un registre quantique. On sait que grâce à la porte de Toffoli, une telle porte \(U_f\) sera tout le temps réalisable.
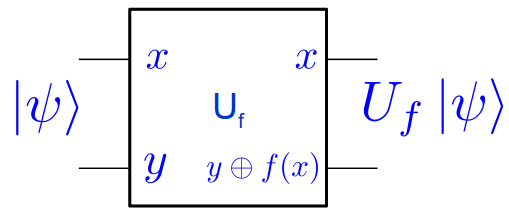
On remarque que le CNOT est un $ U_f $ particulier, pour $ f = I $. De plus, en posant $ \ket{y} = \ket{0} $ on obtient l’équivalent quantique de l’évaluation de la fonction $ f $.
Propriétés
La porte $ U_f $ possède plusieurs propriétés intéressantes.
- La première se nomme le parallélisme quantique. Considérons ce circuit :
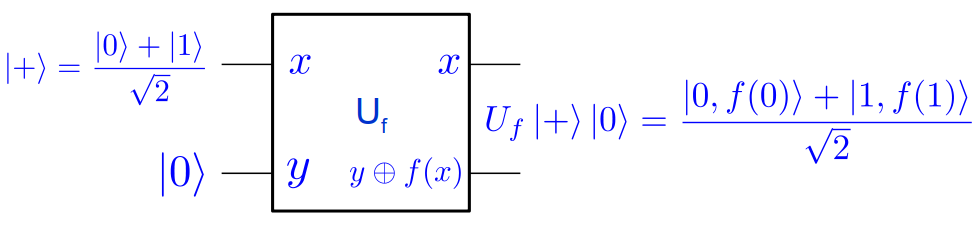Le résultat donne un état clairement intriqué, mais aussi remarquable par le fait qu’il évalue les deux valeurs possibles de f en un seul appel ! Par contre toute mesure de cet état ne pourra permettre de connaître que $ \ket{0,f(0)} $ ou (exclusif) $ \ket{1,f(1)} $ donc le seul parallélisme n’a à ce stade aucune utilité, car ne donnera comme information que l’image de 0 ou (exclusif) 1. - La deuxième propriétés intéressante est l’interférence quantique. Si maintenant on applique $ U_f $ avec $ \ket{y} = \ket{-} $ et $ \ket{x} = \ket{0} $ ou $ \ket{x} = \ket{1} $ on obtient le résultat suivant :
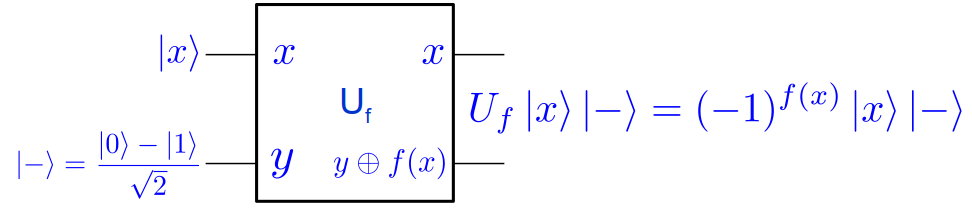On peut démontrer celà en décomposant les calculs.
\(U_f \ket{x} \ket{-} = \frac{U_f \ket{x} \ket{0} - U_f \ket{x} \ket{1}}{\sqrt{2}} = \ket{x} \frac{\ket{0 \oplus f(x)} - \ket{1 \oplus f(x)}}{\sqrt{2}}\)
Or :
\(\frac{\ket{0 \oplus f(x)} - \ket{1 \oplus f(x)}}{\sqrt{2}} = \frac{\ket{0} - \ket{1}}{\sqrt{2}} = \ket{-}\) si $ f(x) = 0 $
\(\frac{\ket{0 \oplus f(x)} - \ket{1 \oplus f(x)}}{\sqrt{2}} = \frac{\ket{1} - \ket{0}}{\sqrt{2}} = -\ket{-}\) si $ f(x) = 1 $
Soit :
\(U_f \ket{x} \ket{-} = (-1)^{f(x)}\ket{x}\ket{-}\)
Donc avec $ \ket{-} $ sur le registre cible l’état obtenu n’est pas intriqué, mais tout se passe comme si c’était le registre de données qui était « marqué » par un déphasage de $ \pi^{f(x)} $.
Ces deux étranges phénomènes sont la clé de tous les algorithmes de recherche quantiques.
Combinaison des propriétés de $U_f$
Il est possible de combiner les deux propriétés de $U_f$, le parallélisme et l’interférence.
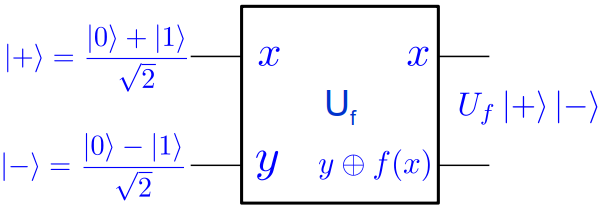On obtient alors :
\(U_f\ket{+}\ket{-} = \frac{U_f\ket{0}\ket{-} + U_f\ket{1}\ket{-}}{\sqrt{2}} = \frac{(-1)^{f(0)}\ket{0} + (-1)^{f(1)}\ket{1}}{\sqrt{2}}\ket{-}\)
Soit :
\(U_f\ket{+}\ket{-} = \ket{+}\ket{-}\)
si $f(0) = f(1) = 0$
\(U_f\ket{+}\ket{-} = -\ket{+}\ket{-}\)
si $f(0) = f(1) = 1$
\(U_f\ket{+}\ket{-} = \ket{-}\ket{-}\)
si $f(0) = 0$ et $f(1) = 1$
\(U_f\ket{+}\ket{-} = -\ket{-}\ket{-}\)
si $f(0) = 1$ et $f(1) = 0$
Finalement, le résultat final est :
\(U_f\ket{+}\ket{-} = \pm\ket{+}\ket{-}\)
si $f(0) = f(1) $
\(U_f\ket{+}\ket{-} = \pm\ket{-}\ket{-}\)
si $f(0) \neq f(1) $
Circuit de l’algorithme
En exploitant ces propriétés, Deutsch propose le circuit suivant, pour savoir si la fonction $f$ est constante ou non.
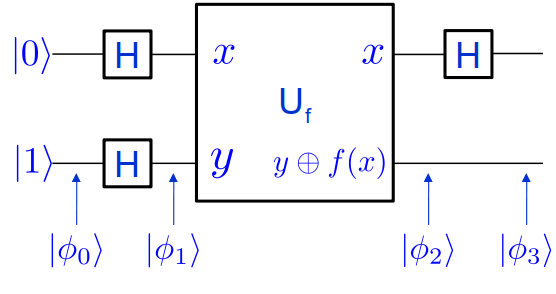Examinons le circuit :
- $ \ket{\phi_0} = \ket{01} $
- $ \ket{\phi_1} = \ket{+-} $, la porte de Hadamard faisant passer dans la base X
- D’après la section précédente :
$ \ket{\phi_2} = \pm\ket{+-} $ si $ f(0) = f(1) $
$ \ket{\phi_2} = \pm\ket{--} $ si $ f(0) \neq f(1) $ - La porte de Hadamard fait repasser le premier qubit dans la base standard :
$ \ket{\phi_3} = \pm\ket{0-} $ si $ f(0) = f(1) $
$ \ket{\phi_3} = \pm\ket{1-} $ si $ f(0) \neq f(1) $
De manière concise : $\ket{\phi_3} = \pm\ket{f(0) \oplus f(1)}\ket{-}$
Donc en un seul appel de la fonction $f$, l’algorithme calcule $f(0)$ mais également $f(1)$ ! On peut alors déterminer si elle est constante ou non. Il suffit de mesurer le premier qubit de $\ket{\phi_3}$. Pour un algorithme classique il aurait fallu appeler 2 fois la fonction. Cela montre qu’en cumulant le parallélisme et l’interférence, un ordinateur quantique donner un résultat utilisable, plus rapidement qu’un oradinateur classique.
Un simulateur de cet algorithme est donné dans la prochaine page afin de se familiariser avec les principes utilisés.
Une remarquable généralisation à une fonction booléenne de n variables booléennes, mettant encore plus en exergue le gain de rapidité d’un ordinateur quantique, a été découverte par Deutsch et Jozsa en 1992.
Algorithme de Deutsch-Josza
Histoire
L’algorithme de Deutsch-Josza est une généralisation de l’algorithme de Deutsch, découverte en 1992 par David Deutsch et Richard Josza. Il permet de savoir pour une fonction $ f:\{0,1\}^n \rightarrow \{0,1\} $, si elle est constante ou équilibrée (l’algorithme de Deutsch traite le cas n=1). Même si il n’a pas vraiment d’utilité, il pose les bases de nombreux autres algorithmes quantiques, en introduisant notamment l’effet d’interférence quantique. L’algorithme de Shor et de Grover, 2 des plus importants dans le domaine, se sont inspiré du fonctionnement de Deutsch-Josza.
Il est important de noter que l’algorithme de Deutsch-Josza a été fournit à l’origine par les 2 auteurs dans une version moins élaborée que celle étudiée aujourd’hui. Des améliorations proposées par Cleve et coll. ont permis d’obtenir de meilleurs résultats. L’algorithme porte cependant toujours ce nom en l’honneur de l’importance cruciale des techniques qui ont été élaborées par David Deutsch et Richard Josza.
Énoncé du problème
Alice et Bob jouent au jeu suivant :
- Bob choisit secrètement une fonction $ f:\{0,1\}^n \rightarrow \{0,1\} $ (fonction booléenne de n variables booléennes), mais a promis à Alice que cette fonction serait :
- Soit constante
- Soit équilibrée (même nombre de valeurs 0 et 1 sur le domaine de définition soit $2^n-1$ valeurs 0 et $2^n-1$ valeurs 1)
- Bob programme sa fonction sur un ordinateur classique, qui rend donc un bit pour chaque donnée d’entrée de n bits.
- Il programme aussi sa fonction grâce à un opérateur unitaire sur $n$ qubits qui rend donc un registre de $n$ qubits pour chaque donnée d’entrée de $n$ qubits.
- Question : Combien faut-il à Alice d’appels de cette fonction dans le cas classique et dans le cas quantique pour déterminer avec certitude si la fonction est constante ou équilibrée ? L’algorithme de Deutsch-Jozsa donne une remarquable solution, mais il faut avant cela quelques préalables…
Transformation de Hadamard
Considérons le circuit ci-contre, qui effectue la transformation notée $H^{\otimes 2} = H \otimes H$ :
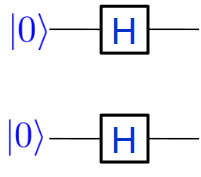on voit facilement que la sortie est $\ket{+}\ket{+} = \frac{\ket{00} + \ket{01} + \ket{10} + \ket{11}}{2}$. Ce calcul se généralise très bien à un cas avec $n$ porte de Hadamard :
\(H^{\otimes n}\ket{0}^{\otimes n} = \frac{1}{\sqrt{2^n}}\sum\limits_{x \in \{0,1\}^n}\ket{x} = \ket{+}^{\otimes n}\)
Cette transformation est appelée transformation de Hadamard et produit une égale superposition de tous les états possibles à $n$ bits (qui n’est évidemment pas un état intriqué).
Parallélisme quantique (cas à $n$ bits)
Si on définit l’opérateur $U_f$ (à l’évidence unitaire) sur $n+1$ bits à partir de la fonction $f$ de $n$ bits de la même manière que pour l’algorithme de Deutsch, on obtient :
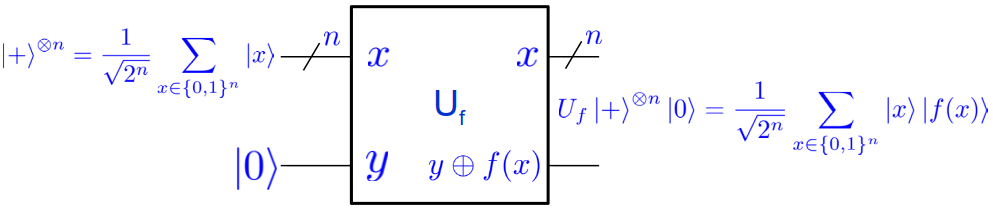On voit que comme le cas à 1 bit, $U_f$ produit un état (clairement intriqué) qui est l’égale superposition des états $\ket{x}\ket{f(x)}$, comme si la fonction était évalué $n$ fois en même temps. Toutefois toute mesure ne permettra d’accéder qu’à un seul d’entre eux.
Interférence quantique (cas à $n$ bits)
Le raisonnement réalisé dans le cas $n=1$ de l’algorithme de Deutsch reste valable. Pour n’importe lequel des $2^n$ $\ket{x}$ de la base de calcul (attention, il faut bien que $\ket{x}$ soit un vecteur de la base), on a :
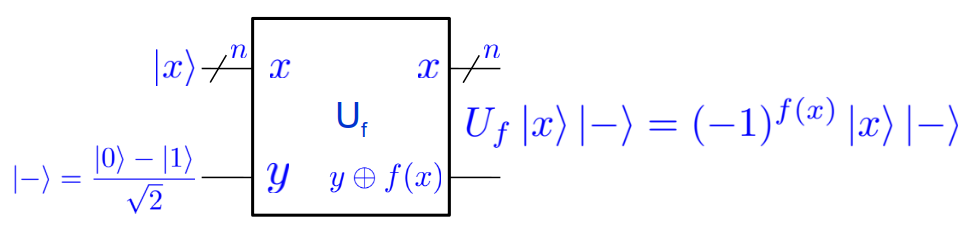Donc comme pour le cas à un bit, avec $\ket{-}$ sur le registre cible, l’état reste inchangé sur le registre cible, mais c’est le registre de données où chaque composante sur un vecteur de base $\ket{x}$ est « marquée » par un déphasage de $\pi^{f(x)}$ !
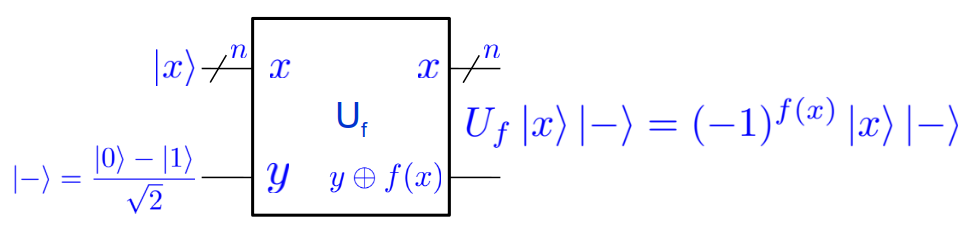Il en résulte comme indiqué dans la figure ci-dessus que :
\(U_f\ket{+}^{\otimes n}\ket{-} = \left[ \frac{ \sum_{x \in \{0,1\}^n}(-1)^{f(x)}\ket{x} }{\sqrt{2^n}} \right] \ket{-}\)
Il s’agit d’une formule très utiles pour les algorithmes de recherches quantiques (colle l’algorithme de Grover).
Algorithme de Deutsch-Josza
Considérons le circuit ci-dessous qui est le circuit de l’algorithme.
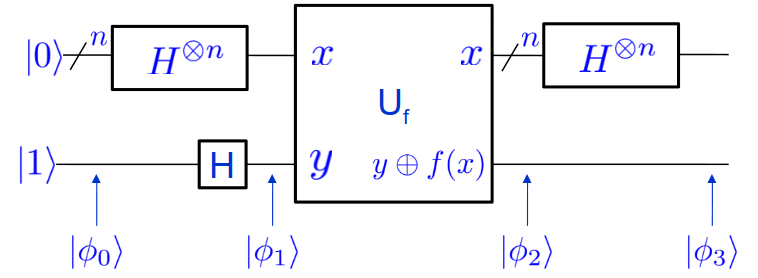Ce qui précède montre que :
- $\ket{\phi_0} = \ket{0}^{\otimes n}\ket{1}$
- $\ket{\phi_1} = \ket{+}^{\otimes n}\ket{-} = \left[ \frac{ \sum_{x \in \{0,1\}^n}\ket{x} }{\sqrt{2^n}} \right] \ket{-}$
- $\ket{\phi_2} = \left[ \frac{ \sum_{x \in \{0,1\}^n}(-1)^{f(x)}\ket{x} }{\sqrt{2^n}} \right] \ket{-}$ Il reste à appliquer la porte $H^{\otimes n} \otimes I$ sur $\ket{\phi_2}$.
Commençons par remarquer que l’action d’Hadamard sur un qubit $H\ket{0} = \frac{\ket{0}+\ket{1}}{\sqrt{2}}$ ou $H\ket{1} = \frac{\ket{0}-\ket{1}}{\sqrt{2}}$ peut se résumer ainsi :
\(H\ket{x} = \frac{ \sum_{z \in \{0,1\}} (-1)^{xz}\ket{z} }{ \sqrt{2} }, x \in \{0,1\}\)
Si l’on généralise, on peut ainsi montrer que pour tout vecteur de la base de calcul à $n$ qubits :
\(H^{\otimes n}\ket{x} = \frac{ \sum_{z_1,...,z_n \in \{0,1\}} (-1)^{x_1z_1 + ... + x_2z_2}\ket{z_1}\otimes ... \otimes\ket{z_n} }{ \sqrt{2^n} }\)
avec \(\ket{x} = \ket{x_1, ..., x_n} = \ket{x_1} \otimes ... \otimes \ket{x_n}, x_i \in \{0,1\}\)
On peut écrire cette équation plus succintement :
\(H^{\otimes n}\ket{x} = \frac{ \sum_{z_1,...,z_n \in \{0,1\}} (-1)^{x \bullet z}\ket{z} }{ \sqrt{2^n} }\)
où $\bullet$ désigne la somme modulo 2 des produits bit à bit.
Grâce à cette formule, on peut désormais calculer $\ket{\phi_3}$ :
\(\ket{\phi_3} = H^{\otimes n} \otimes I\ket{\phi_2} = H^{\otimes n} \otimes I \left[ \frac{ \sum_{x \in \{0,1\}^n}(-1)^{f(x)}\ket{x} }{\sqrt{2^n}} \right] \ket{-}\)
soit \(\ket{\phi_3} = \left[ \frac{ \sum_{x \in \{0,1\}^n}(-1)^{f(x)}H^{\otimes n}\ket{x} }{\sqrt{2^n}} \right] \ket{-}\)
et enfin \(\ket{\phi_3} = \left[ \frac{ \sum_{x,z \in \{0,1\}^n}(-1)^{x \bullet z + f(x)}\ket{z} }{2^n} \right] \ket{-}\)
Grâce à la valeur finale du registre on peut enfin donner une remarquable solution au problème de Deutsch : Alice va effectuer une mesure sur le registre de données.
La formule précédente de $\ket{\phi_3}$ montre que la composante de ce registre sur le vecteur de base \ket{0}^{\otimes n}$ vaut :
\(\alpha_0 = \sum\limits_{x \in \{0,1\}^n}\frac{(-1)^{f(x)}}{2^n}\)
Donc :
- Si la fonction est équilibrée les valeurs 1 et -1 s’équilibrent, $\alpha_0 = 0$ et l’état après la mesure ne peut pas être \(\ket{0}^{\otimes n}\).
- Mais si la fonction est constante il n’y a que des valeurs 1 ou -1 donc $\alpha_0 = 1$ ou $\alpha_0 = -1$ et l’état après la mesure est forcément $\ket{0}^{\otimes n}$ (puisque $|\alpha_0|^2$, soit la probabilité d’obtenir cet état, vaut 1). Donc Alice a une réponse certaine avec seulement un appel de la fonction alors qu’il en faut $2^{n-1}+1$ dans le cas classique !
Conclusion
Le gain de l’ordinateur quantique par rapport à l’ordinateur classique est impressionnant sur ce problème (1 seul appel contre $2^{n-1}+1$ soit un gain exponentiel).
Cela dit le problème de Deutsch n’a aucun intérêt pratique (on ne lui connaît aucune application). De plus la valeur $2^{n-1}+1$ est un pire cas très improbable : dès qu’Alice obtient deux valeurs différentes (ce qui est rapidement probable au bout de quelques appels si la fonction est équilibrée) Alice a aussi une certitude.
Il n’en reste pas moins que l’algorithme de Deutsch-Jozsa eût un rôle fondateur dans l’illustration de l’intérêt du calcul quantique et contient le germe d’algorithmes plus utiles (en particulier les algorithmes de recherche).