Qu’est-ce qu’une porte quantique ?
Produit tensoriel
Afin de manipuler deux qubits (qui pourront être liés ce qui sera l’un des intérêts principaux en informatique quantique), il est nécessaire de définir un espace des états global pour le système de deux qubits.
Cet espace, de dimension 4 est construit à partir des espaces d’états \(\varepsilon_1\) et \(\varepsilon_2\) de chaque bit par l’opération appelée produit tensoriel : \(\varepsilon = \varepsilon_1 \bigotimes \varepsilon_2\)
A tout couple \(\ket{\psi_1}\) et \(\ket{\psi_2}\) de \(\varepsilon_1\) et \(\varepsilon_2\)
est associé un vecteur de \(\varepsilon\) noté \(\ket{\psi_1} \bigotimes \ket{\psi_2}\)
ou plus simplement \(\ket{\psi_1} \ket{\psi_2}\) voire \(\ket{\psi_1 \psi_2}\) appelé produit tensoriel de \(\ket{\psi_1}\) et \(\ket{\psi_2}\)
(dans notre cas les vecteurs de base seront notés \(\ket{00}\), \(\ket{01}\), \(\ket{10}\), \(\ket{11}\))
Trois propriétés importantes:
\(\forall \lambda \in \mathbb{C} : (\lambda \ket{\psi_1}) \bigotimes \ket{\psi_2} = \ket{\psi_1} \bigotimes (\lambda \ket{\psi_2}) = \lambda (\ket{\psi_1} \bigotimes \ket{\psi_2})\)
\((\ket{\psi_1} + \ket{\phi_1}) \bigotimes \ket{\psi_2} = \ket{\psi_1} \bigotimes \ket{\psi_2} + \ket{\phi_1} \bigotimes \ket{\psi_2}\)
\(\ket{\psi_1} \bigotimes (\ket{\psi_2} + \ket{\phi_2}) = \ket{\psi_1} \bigotimes \ket{\psi_2} + \ket{\psi_1} \bigotimes \ket{\phi_2}\)
Intrication quantique
lien vers la page wiki de l’intrication
Selon les trois propriétés de produit tensoriel, certains vecteurs de \(\varepsilon\) peuvent être séparés en produits tensoriels de vecteurs de \(\varepsilon_1\) et \(\varepsilon_2\) mais pas tous, exemple avec deux qubits :
\((\alpha\ket{0} + \beta\ket{1}) \bigotimes (\gamma\ket{0} + \delta\ket{1}) = \alpha\gamma\ket{00} + \alpha\delta\ket{01} + \beta\gamma\ket{10} + \beta\delta\ket{11}\)
Mais il n’existe aucun quadruplet (\(\alpha,\beta,\gamma,\delta\)) de nombres complexes permettant de mettre sous cette forme l’état (un des états dits de Bell) : \({1 \over \sqrt{2}}(\ket{01}+\ket{10})\)
(pas possible d’avoir \(\begin{cases} \alpha\gamma = 0\\\\ \alpha\delta = {1 \over \sqrt{2}}\\\\ \beta\gamma = {1 \over \sqrt{2}}\\\\ \beta\delta = 0 \end{cases}\) en même temps)
De tels états sont dits intriqués.
Introduction des portes à 2 qubits
Cette partie se concentre sur les portes quantiques prenant deux qubits en entrée.
Opérateurs à deux bits (cas classiques)
Il existe 8 fonctions Booléennes de deux variables Booléennes dont deux (les deux fonctions constantes) appelées CLEAR (constante 0) et SET (constante 1) et il reste 6 fonctions (AND, NAND, OR, NOR, XOR, XNOR) qui peuvent être construites à partir du OR (ou du AND) et du NOT
| A | B | AND | NAND | OR | NOR | XOR | XNOR |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
CNOT
La porte NOT contrôlée (également appelée C-NOT ou CNOT) est une porte logique quantique qui constitue un élément essentiel de la construction d’un ordinateur quantique à base de portes. Tout circuit quantique peut être simulé avec un degré de précision arbitraire en utilisant une combinaison de portes CNOT et de rotations d’un seul qubit (X, Y, Z, H, etc).
La porte CNOT permet d’opérer un NOT sur le second bit quantique d’entrée à condition que le premier bit quantique d’entrée soit égal à \(\ket{1}\); dans tous les autres cas, le second bit quantique est laissé inchangé. On nomme ainsi le premier bit quantique d’entrée qubit de contrôle. Le second est en général nommé qubit cible. Cette porte quantique est notamment utilisée pour implémenter l’intrication quantique entre le qubit cible et l’un des qubits de sortie.
Notation abrégée :
\(CNOT : (x,y) \leftrightarrow (x,x \bigoplus y)\)
Matrice de transformation :
\(CNOT \equiv \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}\)
L’effet du CNOT sur un état quelconque :
\(\alpha_{00} \ket{00} + \alpha_{01} \ket{01} +\alpha_{10} \ket{10} +\alpha_{11} \ket{11} \rightarrow \alpha_{00} \ket{00} + \alpha_{01} \ket{01} +\alpha_{10} \ket{11} +\alpha_{11} \ket{10}\)
Circuit :
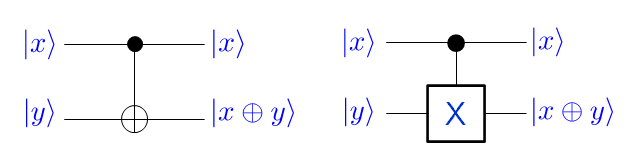
Essayez-le dans le playground :
I-X#0-I-I-I-I
I-X#1-I-I-I-I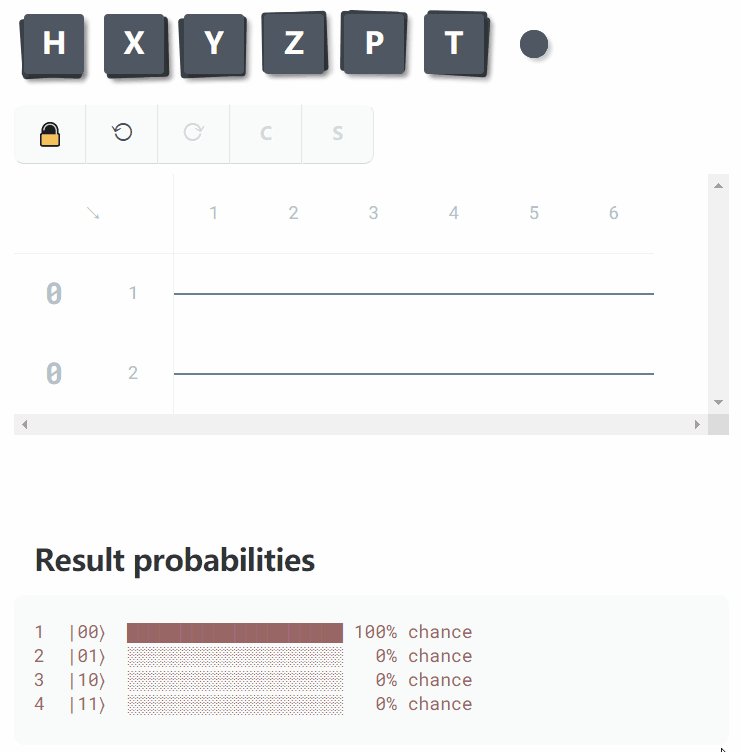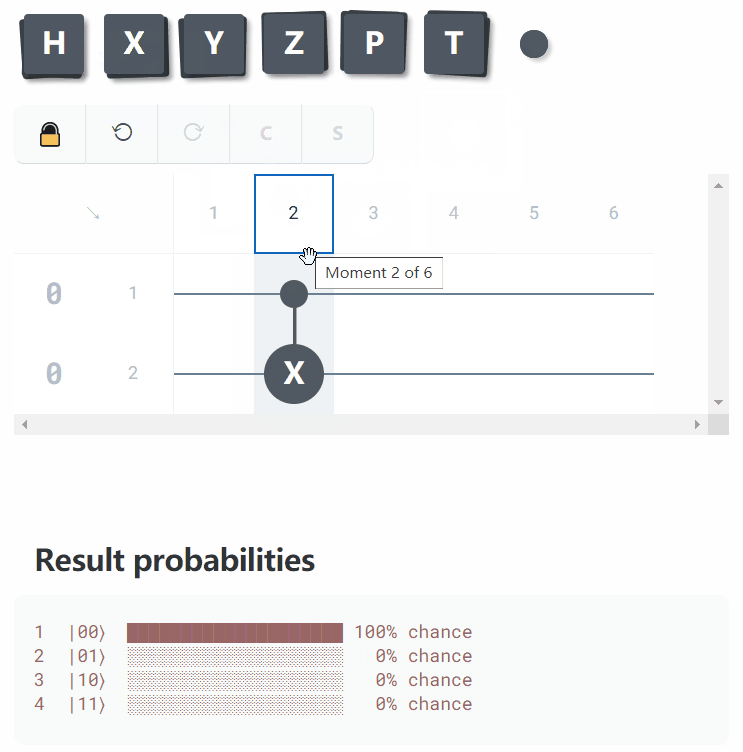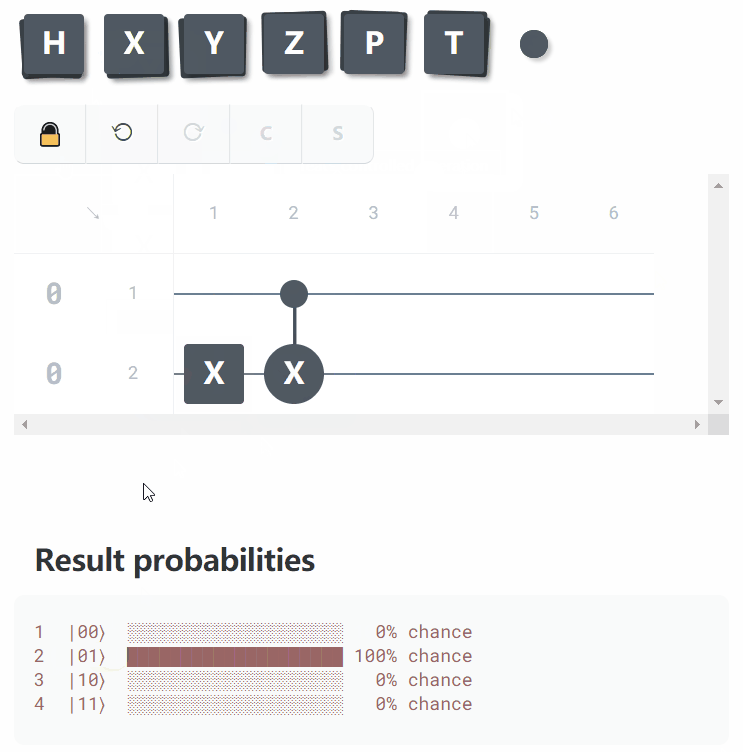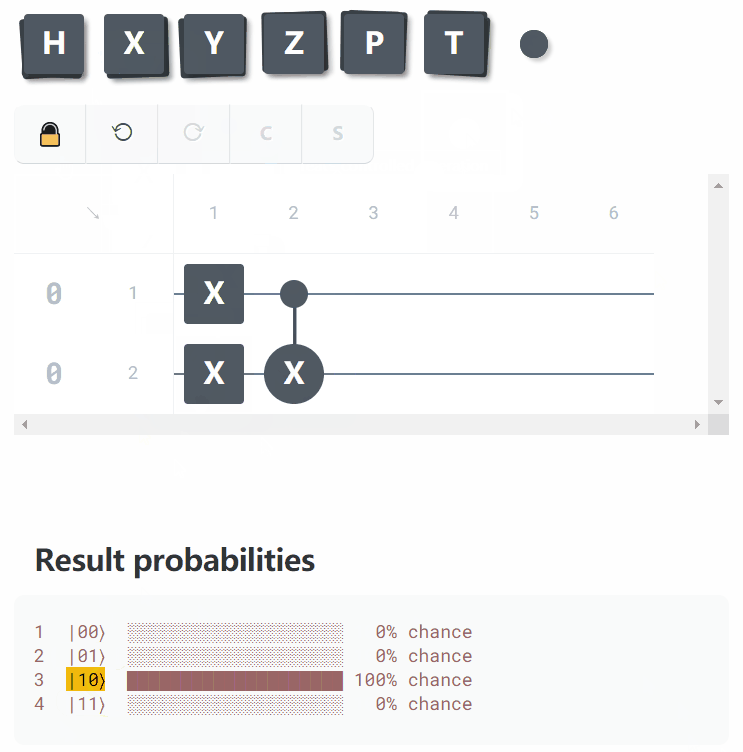
- Exercice :
Démontrer les deux circuits suivants sont égales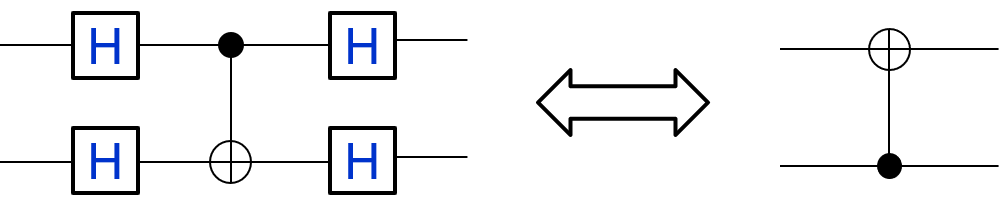 Vous pouvez le vérifier dans le playground :
Vous pouvez le vérifier dans le playground :
Circuit 1
H-X#0-H-I-I-I
H-X#1-H-I-I-ICircuit 2
I-X#1-I-I-I-I
I-X#0-I-I-I-I- Attention :
Dans une opération contrôlée, le fait que le bit de contrôle ne change pas n’est vrai que dans la base de calcul, exemple :
Bleu : Etat initial
Rouge : Après l'opération CNOT
\(\color{blue}{\ket{0}\ket{-}}\) \(= {1 \over \sqrt{2}}(\ket{00}-\ket{01}) \rightarrow \color{red}{\ket{0}\ket{-}}\)
\(\color{blue}{\ket{1}\ket{-}}\) \(= {1 \over \sqrt{2}}(\ket{10}-\ket{11}) \rightarrow {1 \over \sqrt{2}}(\ket{11}-\ket{10}) =\) \(\color{red}{-\ket{1}\ket{-}}\)
\(\color{blue}{\ket{0}\ket{+}}\) \(= {1 \over \sqrt{2}}(\ket{00}+\ket{01}) \rightarrow \color{red}{\ket{0}\ket{+}}\)
\(\color{blue}{\ket{1}\ket{+}}\) \(= {1 \over \sqrt{2}}(\ket{10}+\ket{11}) \rightarrow {1 \over \sqrt{2}}(\ket{11}+\ket{10}) =\) \(\color{red}{\ket{1}\ket{+}}\)
soit sous forme compacte (x=0 ou 1) :
\(\ket{x}\ket{-} \rightarrow (-1)^x \ket{x}\ket{-}\)
\(\ket{x}\ket{+} \rightarrow \ket{x}\ket{+}\)
Il s’ensuit que :
\(\ket{+}\color{red}{\ket{+}}\) \(\rightarrow \ket{+}\ket{+}\)
\(\ket{-}\color{red}{\ket{+}}\) \(\rightarrow \ket{-}\ket{+}\)
\(\ket{+}\color{red}{\ket{-}}\) \(\rightarrow \ket{-}\ket{-}\)
\(\ket{-}\color{red}{\ket{-}}\) \(\rightarrow \ket{+}\ket{-}\)
Conclusion dans la base (\(\ket{+}\), \(\ket{-}\)), les rôles des deux bits sont inversés !
Cet étrange couplage qui n’est pas l’intrication (aucun des états précédent n’est intriqué) est un phénomène d’interférence quantique, utilisé dans tous les algorithmes quantiques utiles, nous y reviendrons…