Les portes quantiques à 1 qubit
Porte quantique - définition
Une porte quantique est un opérateur, qui va faire évoluer le système quantique d’un état à un autre. Concrètement, il s’agit d’un opérateur $U(t,t’)$ de l’équation de Schrödinger qui fait évoluer le système à l’instant $t$ vers un autre système à l’instant $t’$.
Une porte quantique doit donc être Hermitienne d’après les postulats, mais également unitaire pour conserver la somme des probabilités. La matrice d’un opérateur unitaire se caractérise par le fait que ses vecteurs colonnes (ou lignes) ont une norme 1 et sont orthogonaux (au sens du produit scalaire Hermitien).
Les matrices de Pauli
Les matrices de Pauli X, Y et Z forment 3 portes quantiques très utiles.
La matrice X
La porte X peut-être considérée comme l’équivalent quantique du NOT classique.
\(X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\)
En effet, \(X\begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} b \\ a \end{pmatrix}\). Soit :
\(\ket{\psi} = a\ket{0} + b\ket{1},\)
\(X\ket{\psi} = \ket{\psi'}\)
\(avec \ket{\psi'} = b\ket{0} + a\ket{1}\)
Les probabilités sont donc inversées.
Les matrices Y et Z
Les matrices Y et Z s’écrivent :
\(Y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}, Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\)
Rapport avec la sphère de Bloch
On trouve (ou vérifie) très facilement les vecteurs propres de X, Y et Z pour les valeurs propres +1 et -1 sont respectivement :
- $\ket{+}$ et $\ket{-}$ pour X donc états correspondants au vecteurs de Bloch $\pm\vec{x}$.
- $\ket{+i}$ et $\ket{-i}$ pour Y donc états correspondants au vecteurs de Bloch $\pm\vec{y}$.
- $\ket{0}$ et $\ket{1}$ pour Z donc états correspondants au vecteurs de Bloch $\pm\vec{z}$. d’où les noms donnés à ces matrices. Il s’agit des états particuliers de la sphère cités précédemment.
Chacun de ces couple de vecteur des états peuvent former une base de l’espace des états $\mathcal{E}$. Dans chacune de ces bases (notées également X, Y, et Z par abus de langage) l’opérateur de même nom a donc pour matrice :
\(\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}\),
base X : \((\ket{+}, \ket{-})\)
base Y : \((\ket{+i}, \ket{-i})\)
base Z : \((\ket{0}, \ket{1})\)
Effet des opérateurs X, Y, Z
L’opérateur Z transforme un vecteur $\ket{\psi}$ en $Z\ket{\psi} = cos(\frac{\theta}{2})\ket{0} - e^{i\phi}sin(\frac{\theta}{2})\ket{1}$. Il s’agit d’une rotation du vecteur de Bloch d’un angle $\pi$ autour de l’axe z. Les opérateurs X et Y ont le même effet, respectivement autour des axes x et y.
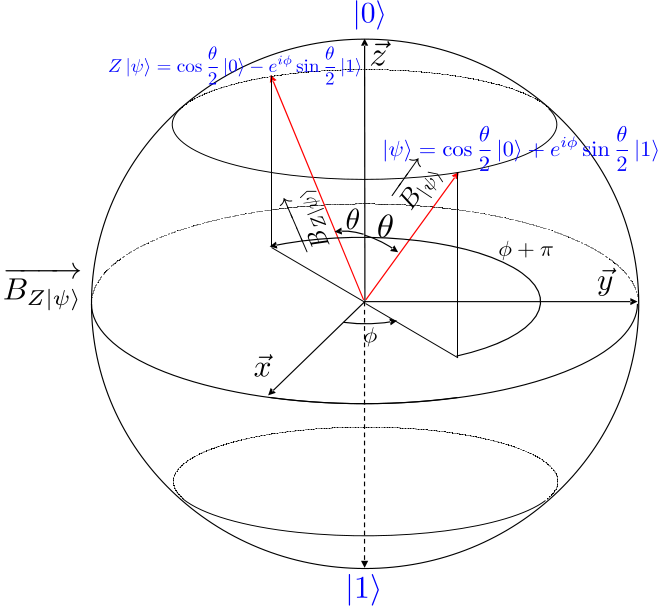Effet de la matrice Z sur l’état d’un qubit : rotation d’un angle $\pi$ autour de l’axe $\vec{z}$
Operateurs rotation
Les opérateurs rotation permettent d’appliquer une rotation du vecteur de Bloch d’un angle $\alpha$ autour d’un des 3 axes x, y ou z de la sphère.
\(R_x(\alpha) = \begin{pmatrix} cos(\frac{\alpha}{2}) & -isin(\frac{\alpha}{2}) \\ -isin(\frac{\alpha}{2}) & cos(\frac{\alpha}{2}) \end{pmatrix}, R_y(\alpha) = \begin{pmatrix} cos(\frac{\alpha}{2}) & -sin(\frac{\alpha}{2}) \\ sin(\frac{\alpha}{2}) & cos(\frac{\alpha}{2}) \end{pmatrix}, R_z(\alpha) = \begin{pmatrix} e^{-i\alpha/2} & 0 \\ 0 & e^{i\alpha/2} \end{pmatrix}\)
Ces matrices sont données dans la base de calcul dite base Z où la matrice de l’opérateur Z est diagonale, donc également celle de $R_z(\alpha)$. Il est bien clair que les opérateurs $R_x(\alpha)$ et $R_y(\alpha)$ auraient la même matrice respectivement dans les bases X et Y.
L’effet de l’opérateur $R_z(\alpha)$ est donc :
\(R_z(\alpha) = \begin{pmatrix} e^{-i\alpha/2} & 0 \\ 0 & e^{i\alpha/2} \end{pmatrix} \begin{pmatrix} cos(\frac{\theta}{2}) \\ e^{i\phi}cos(\frac{\theta}{2}) \end{pmatrix} = e^{-i\alpha/2} \begin{pmatrix} cos(\frac{\theta}{2}) \\ e^{i(\phi+\alpha)}cos(\frac{\theta}{2}) \end{pmatrix}\)
Le facteur de phase $e^{-i\alpha/2}$ n’influant pas sur le vecteur de Bloch, cela correspond donc à une rotation autour de l’axe z du vecteur de Bloch d’un angle $\alpha$.
Bien que X, Y et Z tournent le vecteur de Bloch de $\pi$ autour de x, y et z, ils ne sont pas pour autant $R_x, R_y$ et $R_z$ ! En effet :
\(X = iR_x(\pi), \enspace Y = iR_y(\pi), \enspace Z = iR_z(\pi)\)
Plus globalement: tout opérateur unitaire de $\mathcal{E}$ peut se mettre sous la forme d’une combinaison d’une rotation et d’un facteur de phase. Chaque porte permet donc d’effectuer une rotation du vecteur de Bloch d’une certaine quantité.
La porte Hadamard
La porte Hadamard est très utile car elle permet de préparer un qubit dans un état superposé.
\(H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}\)
On peut voir que $H\ket{0} = \ket{+}$ et $H\ket{1} = \ket{-}$, ce qui transforme un état non superposé en un état superposé.
On peut vérifier que les vecteurs propres de H sont $cos(\frac{\pi}{8})\ket{0} + sin(\frac{\pi}{8})\ket{1}$ et $sin(\frac{\pi}{8})\ket{0} - cos(\frac{\pi}{8})\ket{1}$. H est la rotation de $\pi$ autour de cet axe (au facteur de phase $i$ près comme X, Y et Z).
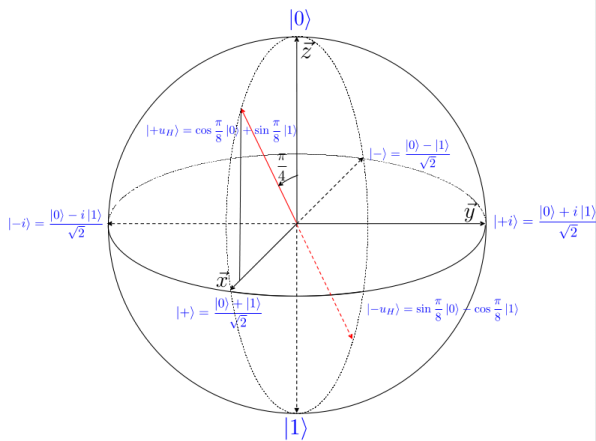En rouge, axe de la rotation causé par l’opérateur Hadamard
Dans la page suivante, une sphere de bloch interactive est disponible afin d’observer les effets des différents opérateurs quantiques.