Introduction à la physique quantique
Genèse de la physique quantique
Newton considérait la lumière comme un flux de particules matérielles et s’opposait ainsi à Huyghens qui y voyait une onde. Les lois de l’optique géométrique ont en effet des interprétations mécanistes ou ondulatoires.
Les équations de Maxwell (1865) qui unifie électricité et magnétisme semblaient conclure la question en considérant la lumière comme un rayonnement faisant parties des ondes électromagnétiques.
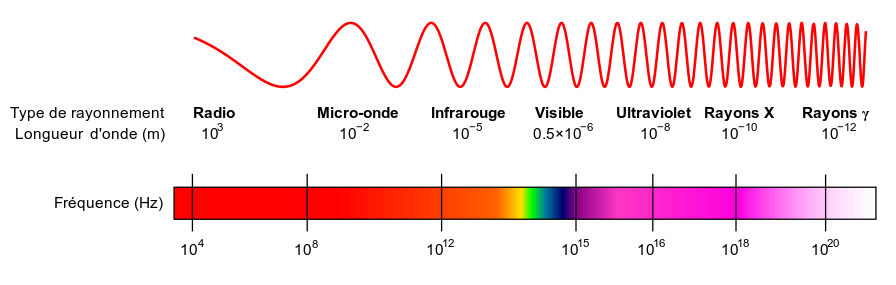 Les différentes catégories d’ondes électromagnétiques
Les différentes catégories d’ondes électromagnétiques
Cependant, deux découvertes remirent en question cet aspect ondulatoire du visible.
- L’étude du rayonnement du corps noir : Un corps noir désigne un objet idéal absorbant parfaitement l’énergie électromagnétique à laquelle il est soumis, ce qui a pour effet d’augmenter sa température et d’émettre un rayonnement appelé rayonnement de corps noir. La mécanique classique, mise à mal pour décrire ce type d’objet, prévoyait l’émission d’une quantité infinie d’énergie : c’est la catastrophe ultraviolette. Afin de résoudre ces aberrations, Max Planck introduisit le concept de quantum en 1900 : l’énergie n’est pas émise de manière continue mais de manière discrète et ne peut prendre que certaines valeures bien précises. Beaucoup essayèrent de trouver une explication non quantique à ce problème dont Planck lui-même, avant de se résoudre à accepter un tel phénomène.
- L’effet photo-électrique : Cet effet désigne l’émission d’un courant électrique pour certains matériaux après avoir été soumis à la lumière. Cet effet étrange fut expliqué par Einstein en 1905 qui s’inspira de l’idée de Planck et introduisit un quantum d’énergie lumineuse. Cette explication conclue à des comportements corpusculaires de la lumière. Ce quantum sera plus tard considéré comme une particule et appelé photon, en 1926.
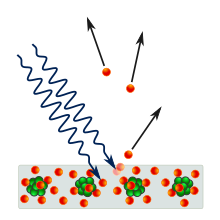 Effet photoélectrique, l’absorption de photons (en bleu) d’une certaine énergie entraine la libération d’électrons (en rouge). Source : Wikipédia
Effet photoélectrique, l’absorption de photons (en bleu) d’une certaine énergie entraine la libération d’électrons (en rouge). Source : Wikipédia
L’introduction de cette discrétisation des valeurs d’énergies possibles fonde la base de du principe de dualité onde-corpuscule qui stipule que tous les objets physiques peuvent présenter parfois des proriétés d’ondes, parfois des propriétés corpusculaires.
Ainsi, la réalité veut que le monde de l’infiniment petit soit discret et quantifié. Cette conséquence posa les bases de la mécanique quantique et permit d’expliquer de nombreux phénomènes alors inexpliquables par la physique classique.
Les postulats de la mécanique quantique
L’expérience des Fentes d’Young
L’expérience des fentes d’Young permet de comprendre certains phénomènes étranges intervenant dans le monde de l’infiniment petit.
Cette expérience consiste à diviser un faisceau lumineux en deux en le faisant passer par deux fentes très petites, puis d’observer le résultat sur un écran. Les deux faisceaux créés interfèrent alors, créant des zones de lumières aux endroits où l’interférence est constructive et des zones sombres aux endroits où l’interférence est destructive.
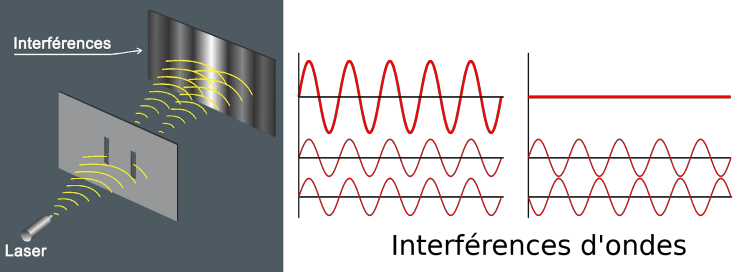 Expérience des fentes de Young. La différence de distance parcourue crée des interférences destructives (franges noires) ou constructives (frange blanches).
Expérience des fentes de Young. La différence de distance parcourue crée des interférences destructives (franges noires) ou constructives (frange blanches).
Cette expérience réalisée en 1801 par Thomas Young constituait l’argument principal défendant la nature ondulatoire de la lumière. On est aujourd’hui capable de la refaire en émettant les photons un par un dans le dispositif. Que se passe-t-il alors ? Une simulation de l’expérience 3 est disponible sur le site.
La figure suivante montre 4 expériences d’envoi de photon un par un:
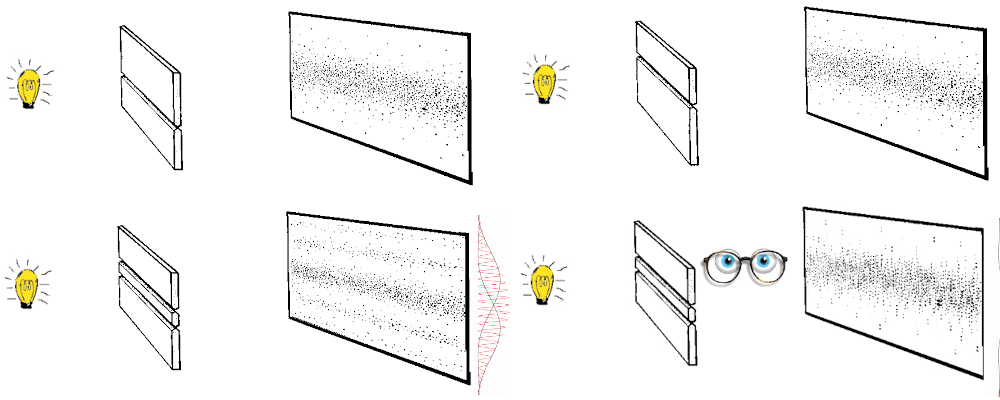 Expérience 1 : photons diffractés par la seule fente 1. Expérience 2 : photons diffractés par la seule fente 2. Expérience 3 : photons diffractés par les fentes 1 et 2. Expérience 4 : Un dispositif tente de mesurer par quelle fente passent les photons.
Expérience 1 : photons diffractés par la seule fente 1. Expérience 2 : photons diffractés par la seule fente 2. Expérience 3 : photons diffractés par les fentes 1 et 2. Expérience 4 : Un dispositif tente de mesurer par quelle fente passent les photons.
- Expérience 1 et 2 : Les photons passent par l’unique fente, on obtient donc un écran rempli d’impacts, car il n’y a pas d’interférences.
- Expérience 3 : Dans l’expérience 3, la mécanique classique nous dit que les photons, envoyé un par un, passent soit par la fente 1 soit par la fente 2. On devrait donc se retrouver avec un écran remplis d’impacts. Pourtant ce n’est pas le cas, on voit apparaître un motif d’interférence, comme si le photon interférait avec lui-même ! Après avoir passé les fentes, le photon se retrouve dans un état superposé. On peut interpréter vaguement ce fait en disant que la particule est passé par les deux fentes en même temps. C’est l’effet de superposition quantique.
- Expérience 4 : Que se passe-t-il si on cherche à détecter par quelle fente la particule « est réellement passée » ? On trouve effectivement que chaque photon passe par soit la fente 1, soit la fente 2 avec une certaine probabilité bien définie. En effet, il est impossible de prédire à l’avance avec certitude si le photon passera par l’une ou l’autre des fentes. Cette étrange propriété de hasard intrinsèque vaudra la fameuse phrase d’Einstein : “Dieu ne joue pas aux dés”. En effet, bien qu’Einstein acceptait la mécanique quantique, il était en conflit avec Niels Bohr sur son interprétation.
Cependant, lors de la mesure, la figure d’interférence disparaît. En effet, l’observateur force le photon à passer par l’une des fentes et détruit son état de superposition, il ne peut plus donc interférer avec lui-même. C’est le principe de réduction du paquet d’onde : l’observateur influe sur le système.
Ces expériences permettent de mettre en avant les étrangetés du monde quantique de l’infiniment petit. Afin de pouvoir les expliquer, les physiciens ont établis une liste de postulats, qui définissent les bases de la théorie quantique. Une anmation
Les 6 postulats
Les 6 postulats de la mécanique quantique ont été créés comme des sortes d’axiomes pour pouvoir expliquer certains résultats.
- Principe de superposition : A tout système peut être associé un espace Hermitien (espace vectoriel sur le corps des complexes de dimension $ n $, $ \mathbb{C}^n $). Cet espace représente l’ensemble des états possibles du système et est noté $ \mathcal{E} $. L’état de ce système à un instant quelconque est entièrement décrit par un vecteur unitaire de cet espace.
On nomme ces vecteurs des kets, notés $ \ket{\psi} $ selon la notation de Dirac. Si $ (\ket{\lambda_1}, …, \ket{\lambda_n}) $ forment une base de $ \mathcal{E} $, alors tout état possible du système s’écrit :
$ \ket{\psi} = a_1\ket{\lambda_1} + … + a_n\ket{\lambda_n} $, avec $ a_1, …, a_n \in \mathbb{C}$ et $ |a_1| + … + |a_n| = 1 $.
Il n’est pas rare de représenter l’état sous la forme d’un vecteur colonne :
$ \ket{\psi} = \begin{pmatrix} a_1 \\ \vdots \\ a_n \\ \end{pmatrix} $
On appelle bra le vecteur conjugué hermitique d’un ket :
$ \bra{\psi} = (\ket{\psi})^\dagger = \begin{pmatrix} a_1^* & … & a_n^* \\ \end{pmatrix} $
La multiplication d’un bra par un ket donne le produit scalaire hermitien, noté :
$ \braket{\psi|\phi} \in \mathbb{R} $
Exemple pour les fentes de Young : On a deux états possible. Soit le photon passe par la fente 1, soit le photon passe par la fente 2. Nos deux états de base sont donc $ \ket{fente1} $ et $ \ket{fente2} $. L’espace $ \mathcal{E} $ comprend toute combinaison linéaire possible de ces deux vecteurs. Le photon se trouve dans un état superposé : $ \ket{\psi} = a\ket{fente1} + b\ket{fente2} $. Le module de $a$ détermine la probabilité pour le photon de passer dans la fente 1, et inversement pour b : $P(fente1) = |a|^2$, $P(fente2) = |b|^2$. On verra dans la page sur les qubits que ce genre de système à 2 états fonde les bases de l’informatique quantique.
- Principe de correspondance : A toute grandeur physique mesurable est associée un opérateur Hermitique appelé « observable ».
Un opérateur est une application (représentable par une matrice donc) qui agit sur un ket pour le faire évoluer, où pour mesurer une grandeur du système, en les multipliant. Mathématiquement :
$ A : \mathcal{E} \rightarrow \mathcal{E} \quad \ket{\psi} \rightarrow A\ket{\psi} $
Un opérateur hermitique est tel que :
$ A^\dagger = A $, avec $ A^\dagger = (A^T)^* $
Un opérateur intéressant est le projecteur. Projecteur sur un ket $\ket{\phi}$ : $P_\phi = \ket{\phi}\bra{\phi}$.
Il projète un ket sur un autre : $P_\phi \ket{\psi} = \ket{\phi}\braket{\phi|\psi} = \braket{\phi|\psi}\ket{\phi}$. On voit bien qu’il s’agit d’un ket proportionnel à $\phi$ puisque $ \braket{\psi|\phi} \in \mathbb{R} $. On a donc projeté $ \ket{\psi} $ sur $ \ket{\phi} $.
Exemple pour les fentes de Young : Calcul du projecteur sur l’état $\ket{fente1}$. Un tel opérateur représente en quelque sorte la grandeur mesurable le photon passe par la fente 1.
\(P_{fente1} = \ket{fente1}\bra{fente1} = \begin{pmatrix} 1 \\\ 0 \end{pmatrix} \begin{pmatrix} 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\\ 0 & 0 \end{pmatrix}\)
-
Principe de quantification : La mesure de la grandeur physique associée à un opérateur A ne peut donner qu’une des valeurs propres (valeur réelle car A est Hermitique) $a_n$ de A Exemple pour les fentes de Young : Si l’on regarde le projecteur précédemment calculé, on obtient 2 résultats possibles : 1 ou 0, soit en traduction littéral le photon est passé par la fente 1 ou le photon n’est pas passé par la fente 1.
-
L’intervention du hasard : Lorsque l’on mesure la grandeur physique associée à un opérateur A, d’un système dans un état $\ket{\psi}$ la probabilité d’obtenir comme résultat la valeur propre $a_n$ est le carré de la norme de la projection de $\ket{\psi}$ sur l’espace propre $\mathcal{E} _{a_n}$ associé à $a_n$. Ce postulat montre que le monde quantique est intrinsèquement probabiliste. Les résultats obtenus représentent toujours des probabilités, on ne peut pas prédire un évènement avec certitude (sauf si la probabilité vaut 1 dans certains cas). Mathématiquement, en notant le projecteur correspondant $P_n$:
\(Proba(a_n) = ||P_n\ket{\psi}||^2 = \bra{\psi}P_n^\dagger P_n\ket{\psi} = \bra{\psi}P_n\ket{\psi}\)
Exemple pour les fentes de Young : Poursuivons notre calcul avec le projecteur sur $\ket{fente1}$. L’observable utilisé ici est le projecteur lui-même. Calculons la probabilité d’obtenir la valeur 1 pendant la mesure. L’espace propre associé à la valeur propre 1 de notre observable est $\ket{fente1}$. $P_n$ représente donc ici le projecteur sur $\ket{fente1}$ (attention : on utilise ici le projecteur en tant qu’observable ET projecteur). Notre photon est dans l’état $ \ket{\psi} = a\ket{fente1} + b\ket{fente2} $.
\(Proba(1) = \bra{\psi}P_{fente1}\ket{\psi}\)
\(= \begin{pmatrix}
a^* & b^*
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\\
0 & 0
\end{pmatrix}
\begin{pmatrix}
a \\\
b
\end{pmatrix}\)
\(= \begin{pmatrix}
a^* & 0
\end{pmatrix}
\begin{pmatrix}
a \\\
b
\end{pmatrix}
= a^* a = |a|^2\)
On retrouve le même résultat qu’évoqué précédemment. La probabilité pour le photon de passer dans la fente 1 est égale au module de $a$ au carré. On peut également calculer la probabilité de mesurer 0, en utilisant le projecteur sur $\ket{fente2}$ (mais toujours avec le projecteur sur $\ket{fente1}$ comme observable). On trouverait comme résultat $|b|^2$.
- Principe de réduction du paquet d’onde : Si la mesure d’une grandeur physique A sur un système, qui se trouvait immédiatement avant la mesure dans l’état $\ket{\psi}$, a donné le résultat $a_n$ alors l’état $\ket{\psi’}$ du système immédiatement après la mesure est la projection normée de $\ket{\psi}$ sur le sous-espace propre associé à $a_n$.
Plus concrètement : la mesure modifie l’état du système quantique mesuré de manière à faire disparaître les probabilités qui ne se sont pas réalisées. L’état du système est modifié et si on le remesure on trouvera encore $a_n$ :
\(\ket{\psi'} = \frac{P_n\ket{\psi}}{\sqrt{\bra{\psi}P_n\ket{\psi}}}\)
Exemple pour les fentes de Young : Supposons que l’on mesure l’observable représenté par le projecteur sur $\ket{fente1}$ et que l’on trouve la valeur 1. Alors l’état du système est désormais
\(\ket{\psi'} = \frac{P_{fente1}\ket{\psi}}{\sqrt{\bra{\psi}P_n\ket{\psi}}}\)
$ = \frac{
\begin{pmatrix}
1 & 0 \\
0 & 0
\end{pmatrix}
\begin{pmatrix}
a \\
b
\end{pmatrix}}
{|a|} $
$ = \frac{1}{|a|}
\begin{pmatrix}
a \\
0
\end{pmatrix} $
On voit bien le système n’est plus superposé car il n’a plus de composante sur $\ket{fente2}$. Il a en revanche une composante sur $\ket{fente1}$ : $a’ = \frac{a}{|a|}$ avec $|a’|^2 = 1$ ce qui montre qu’une nouvelle mesure indiquera que le photon est passé par la fente 1 avec une probabilité de 1.
- Sixième postulat : L’évolution dans le temps du vecteur d’état $\ket{\psi(t)}$ d’un système est régie par l’équation de Schrödinger :
\(ih \frac{d}{dt}\ket{\psi(t)} = H(t)\ket{\psi(t)}\)
où $h$ est la constante de Planck réduite et $H(t)$ est l’observable correspondant à l’énergie du système (hamiltonien). Ce postulat nous indique que, bien que la mesure d’un système soit indéterministe (principe de réduction du paquet d’onde), son évolution dans le temps est parfaitement déterministe et calculable grâce à cet équation différentielle. Ce postulat n’est pas primordial pour la compréhension de l’informatique (mais il l’est pour la réalisation physique des ordinateurs quantiques). Le Hamiltonien contient toute la physique du système considéré (photon, spin 1/2…). L’équation de Schrödinger, si on la résoud, a pour conséquence que l’état $\ket{\psi’}$ à un instant $t’$ peut être déduit de l’état $\ket{\psi}$ à l’instant $t$ par un opérateur $U(t,t’)$ appelé opérateur d’évolution, qui ne dépend que du Hamiltonien.
Dans la page suivante, une simulation de l’expérience des fentes de Young est disponible.