Numerical simulation of bioartificial capsules and cells in flow

Scientific challenges and objectives

In most applications, capsules are suspended in a carrying fluid (Figure 1a). When the suspension is flowing, the particles deform in a complex manner under the hydrodynamic stresses. Modeling the motion and deformation of a capsule in flow is a difficult non-linear problem, as non-conventional fluid-structure interactions intervene: the fluid motion is governed by viscous effects, the structure is undergoing large deformation and inertial effects are negligible. The assumptions that are typically made are:

a b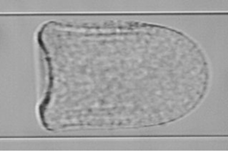

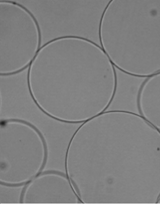
Figure 1: Ovalbumin-membrane capsules. (a) Capsules in suspension in a liquid at rest. (b) Capsule flowing in a tube: folds form in the azimuthal direction (Hu et al. 2012).

• The internal and external fluids are Newtonian and incompressible
• The membrane is infinitely thin and can be treated as a hyperelastic surface
• The internal and external flows are at very small Reynolds numbers and can be described by the Stokes equations

Assuming the capsule wall as an elastic surface without bending rigidity is only valid as long as the membrane is under traction. When the membrane experiences in plane compression in one direction, it tends to fold and buckle, these phenomena being governed by its bending rigidity. The existence of such phenomena has been demonstrated experimentally (figure 1b). The problem is that they tend to make unstable numerical codes based on a membrane model.

The objective has therefore been to develop a new coupling method (solving for the fluid-structure interactions) that remains numerically stable in zones of compression and that has a very precision.

New fluid-structure coupling strategy

We introduce a new numerical method to model the fluid–structure interaction between a microcapsule and an external flow (Walter et al. 2010, Barthès-Biesel et al. 2010). An explicit finite element method is used to model the large deformation of the capsule wall, which is treated as a bidimensional hyperelastic membrane. It is coupled with a boundary integral method to solve for the internal and external Stokes flows. Our results are compared with previous studies in two classical test cases: a capsule in a simple shear flow and in a planar hyperbolic flow. The method is found to be numerically stable, even when the membrane undergoes in-plane compression, which had been shown to be a destabilizing factor for other methods. The stiffness introduced by the numerical method contributes to the stability of the problem because it enriches the membrane model with some bending stiffness. It allows the numerical procedure to remain stable during transient phases when in-plane compression and high curvatures may render other methods unstable. It also has the advantage that steady states with negative tensions can be computed and studied. While it stabilizes the numerical procedure, the stiffness introduced by the elements is a byproduct of the numerical method and cannot be controlled or used to model the physical bending stiffness of a capsule.

The results are in very good agreement with the literature. When the capillary number Ca, ratio of the fluid viscous forces to the membrane elastic forces, is increased, three regimes are found for both flow cases (Figure 2). Our method allows a precise characterization of the critical parameters governing the transitions.

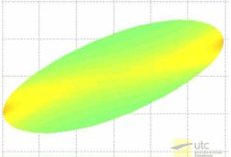a b c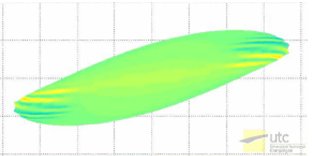

Figure 2: Deformed shape of an initially spherical capsule in a linear shear flow at steady state (neo-Hookean membrane law). Persistence of compressive normal forces at low (a) and high (c) values of the capillary number (Walter et al. 2010).

Influence of internal viscosity on the large deformation and buckling of a spherical capsule in a simple shear flow

We numerically studied the motion and deformation of a spherical elastic capsule freely suspended in a simple shear flow, focussing on the effect of the internal-to-external viscosity ratio (Foessel et al. 2011). For low viscosity ratios, the internal viscosity no longer affects the capsule deformation. Inversely, for large viscosity ratios, the slowing effect of the internal motion lowers the overall capsule deformation; the deformation is asymptotically independent of the flow strength and membrane behaviour. An important result is that increasing the internal viscosity leads to membrane compression and possibly buckling. Above a critical value of the viscosity ratio, compression zones are found on the capsule membrane for all flow strengths. This shows that very viscous capsules tend to buckle easily.

Ellipsoidal capsules in simple shear flow: prolate versus oblate initial shapes

The large deformations of an initially-ellipsoidal capsule in a simple shear flow are studied by coupling a boundary integral method for the internal and external flows and a finite element method for the capsule wall motion. Oblate and prolate spheroids are considered (initial aspect ratios a/b = 0.5 and 2) in the case where the internal and external fluids have the same viscosity. The influence of the membrane mechanical properties (mechanical law, ratio of shear to area dilatation moduli) on the capsule behaviour is investigated.

When the revolution axis of the initial spheroid lies in the shear plane, two regimes are found depending on the value of the capillary number (Walter et al. 2011). As shown in figure 3, the capsule tumbles behaving mostly like a solid particle at low Ca (tumbling regime), while at higher Ca, the capsule has a fluid-like behaviour and oscillates in the shear flow while its membrane continuously rotates around its deformed shape (swinging regime). During the tumbling-to-swinging transition, the capsule transits through an almost circular profile in the shear plane for which a long axis can no longer be defined. The critical transition capillary number is found to depend mainly on the initial shape of the capsule and on its shear modulus, and weakly on the area-dilatation modulus. Qualitatively, oblate and prolate capsules are found to behave similarly, particularly at large capillary numbers when the influence of the initial state fades out. However, the capillary number at which the transition occurs is significantly lower for oblate spheroids.

Figure 3: Evolution of the capsule shape in the shear plane over one half period. The initial shape is a prolate spheroid, a/b = 2, and the membrane follows the Sk law with C = 1. The grey scale corresponds to the normal component of the load. The dot shows the position of material point P, originally on the short axis. (a) Tumbling at low capillary number, (b) Transition, (c) Swinging at higher capillary number (Walter et al. 2011).

The question which arises is whether these results hold when the capsule revolution axis is initially placed off the shear plane. We have investigated the equilibrium regimes that are mechanically stable when the capsule axis is not confined within the shear plane.

In the case of a prolate capsule (Dupont et al. 2013), we have shown that tumbling is unstable and that the capsule instead follows a rolling regime at low capillary number. The swinging regime is, however, stable at very high Ca. In between, the capsule follows a complex motion of precession around the vorticity axis (wobbling regime).

In the case of an oblate capsule (Dupont et al. 2016), tumbling and swinging turn out to be stable until Ca ~ 1 (Figure 4). At higher capillary numbers, the capsule first wobbles until it reorients its revolution axis along the vorticity axis and follows a rolling regime. When the viscosity ratio is increased, the tumbling-to-swinging transition occurs at higher Ca while the swinging-to-rolling transition at lower Ca, so that the swinging regime completely disappears from viscosity ratios about 4. The stable equilibrium regimes are then tumbling or rolling depending on the value of Ca.

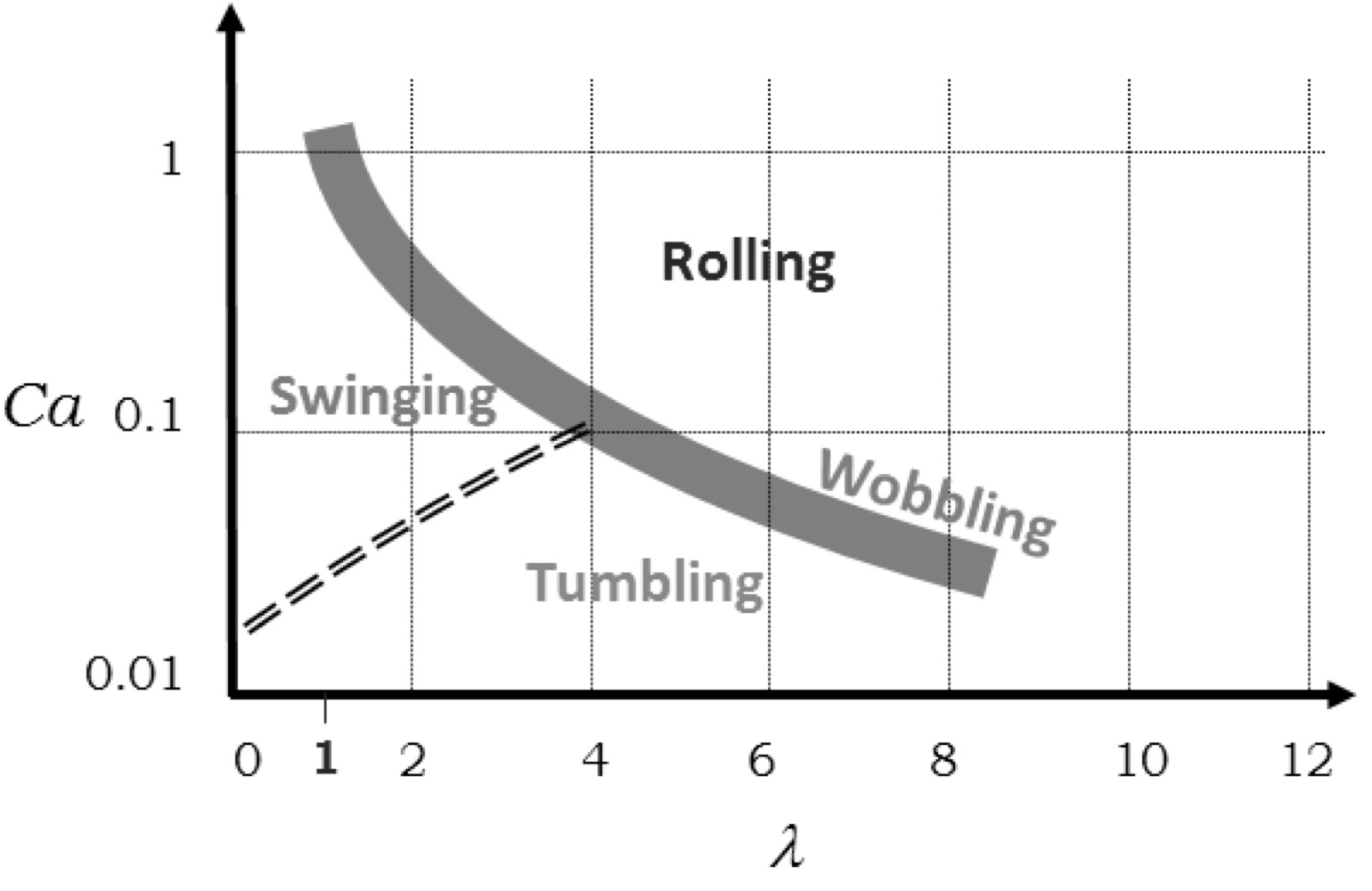
Figure 4: Stable equilibrium regimes for an oblate capsule as a function of the capillary number Ca and viscosity ratio (Dupont et al. 2016).

Bending effect on capsule dynamics

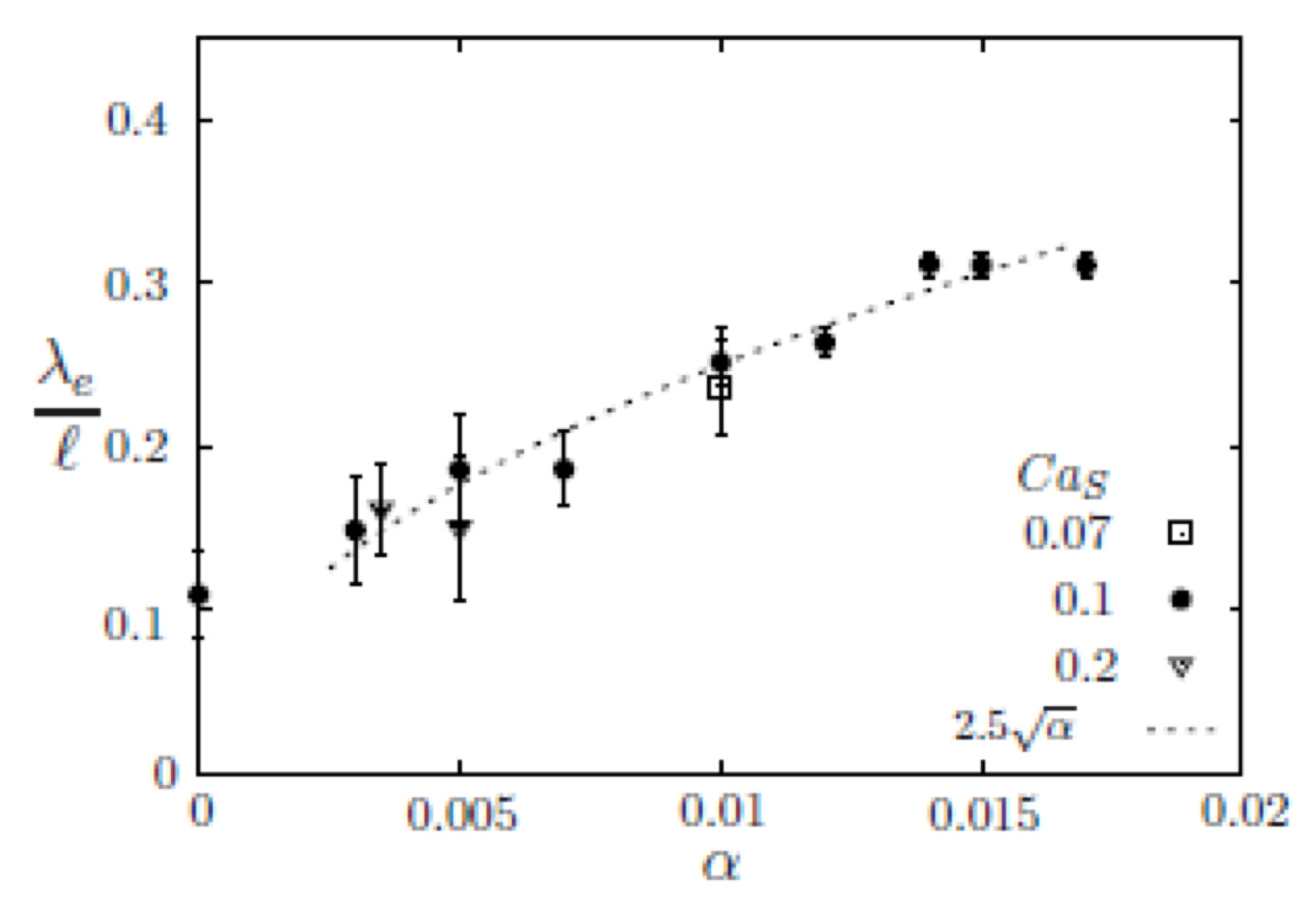
Figure 5: Influence of the ratio α between the wall thickness and capsule diameter on the wavelength λ of the wrinkles in the case of an initially spherical capsule subjected to a simple shear flow (Dupont et al. 2015).

In order to account for bending phenomena and study folding of the capsule wall, a shell finite element method based on MITC elements (Mixed Interpolation of Tensorial Components) have been coupled with the integral boundary method solver (Dupont et al. 2015). We have studied how bending would impact the dynamics of an initially spherical capsule subjected to a simple shear flow.

When the capsule wall is modeled as a three-dimensional shell of finite thickness, a marked decrease in deformability is observed as the thickness increases. But interestingly, if the same results are expressed in terms of the equivalent two-dimensional mechanical properties of the mid-surface, the deformed profile of the capsule is the same as the one predicted for a capsule devoid of bending resistance. The global deformation of an initially spherical capsule is thus governed by elastic deformation, the bending resistance only playing a role locally in regions of wrinkling. Figure 5 indicates that the wrinkle wavelength only depends on the bending non-dimensional number α, which is the ratio of the bending to the elastic forces, or equivalently the ratio between the wall thickness and capsule diameter.

Comparison between spring network models and continuum constitutive laws: application to the large deformation of a capsule in shear flow

Recently, many researchers have used discrete spring network models to express the membrane mechanics of capsules and biological cells. However, it is unclear whether such modeling is sufficiently accurate to solve for capsule deformation. We examined the correlations between the mechanical properties of the discrete spring network model and continuum constitutive laws (Omori et al. 2011). We first compared uniaxial and isotropic deformations of a two-dimensional sheet, both analytically and numerically. The 2D sheet was discretized with four kinds of mesh to analyze the effect of the spring network configuration (Figure 6). We derived the relationships between the spring constant and continuum properties, such as the Young modulus, Poisson ratio, area dilation modulus and shear modulus. It was found that the mechanical properties of spring networks are strongly dependent on the mesh configuration. We then calculated the deformation of a capsule under inflation and in a simple shear flow in the Stokes flow regime, using various membrane models. To achieve high accuracy in the flow calculation, the boundary-element method was used. Comparing the results between the different membrane models, we found that it is hard to express the area incompressibility observed in biological membranes using a simple spring network model.

Figure 6: Configurations of spring network used for the discrete model: cross, cross center, regular triangle, unstructured (Omori et al. 2011).

Flow of a spherical capsule in a pore with circular or square cross-section

a
b

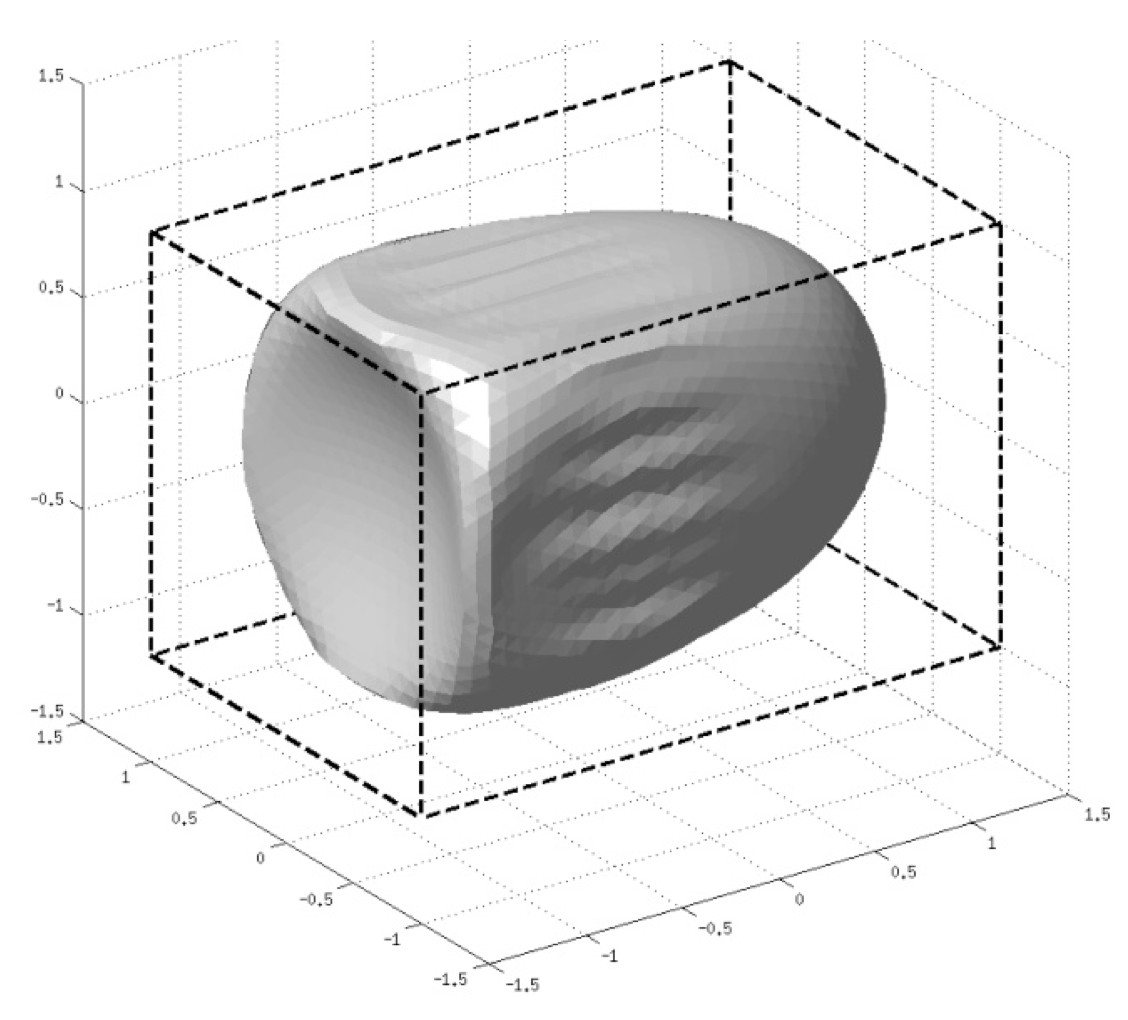
Figure 7: Initially spherical capsule flowing in a a cylindrical or b square-section tube at the same flow rate. The size ratio between the capsule diameter and characteristic size of the channel is 1.1. The capsule wall follows a neo-Hookean law (Hu et al. 2012).

The motion and deformation of a spherical elastic capsule freely flowing in a pore of comparable dimension is studied (Hu et al. 2012). The thin capsule membrane has a neo-Hookean shear-softening constitutive law. The three-dimensional fluid-structure interactions are modelled by coupling a boundary integral method (for the internal and external fluid motion) with a finite element method (for the membrane deformation). In a cylindrical tube with a circular cross-section, the confinement effect of the channel walls leads to compression of the capsule in the hoop direction (figure 7a). The membrane then tends to buckle and to fold as observed experimentally. The capsule deformation is three-dimensional but can be fairly well approximated by an axisymmetric model that ignores the folds. In a microfluidic pore with a square cross-section, the capsule deformation is fully three-dimensional (Figure 7b). For the same size ratio and flow rate, a capsule is more deformed in a circular than in a square cross-section pore. We provide new graphs of the deformation parameters and capsule velocity as a function of flow strength and size ratio in a square section pore. We show how these graphs can be used to analyze experimental data on the deformation of artificial capsules in such channels.

Motion of a spherical capsule in branched tube flow with finite inertia

The transient motion of an initially spherical capsule is considered, when flowing through a right-angled tube bifurcation, composed of tubes having the same diameter (Wang et al. 2017). The capsule motion and deformation is simulated using a three-dimensional immersed-boundary lattice Boltzmann method, with a main focus on the path selection at the bifurcation as a function of the parameters of the problem: the flow split ratio, the background flow Reynolds number Re, the capsule-to-tube size ratio a/R and the capillary number Ca, which compares the viscous fluid force acting on the capsule to the membrane elastic force. For fixed physical properties of the capsule and of the tube flow, the ratio Ca/Re is constant. Two size ratios are considered: a/R = 0:2 and 0.4. At low Re, the capsule favours the branch which receives most flow. Inertia significantly affects the background flow in the branched tube. As a consequence, at equal flow split, a capsule tends to flow straight into the main branch as Re is increased. Under significant inertial effects, the capsule can flow into the downstream main tube even when it receives much less flow than the side branch. Increasing Ca promotes cross-stream migration of the capsule towards the side branch. The results are summarized in a phase diagram, showing the critical flow split ratio for which the capsule flows into the side branch as a function of size ratio, Re and Ca/Re. We also provide a simplified model of the path selection of a slightly deformed capsule and explore its limits of validity. We finally discuss the experimental feasibility of the flow system and its applicability to capsule sorting.

a
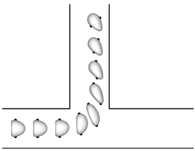
b

Figure 8: Figure 8: Effect of flow split ratio on the path selection of a capsule (a/R = 0.4, Re = 0.25, Ca = 0.5). The successive profiles are plotted in the xz-plane, with 2 dots attached to the membrane to help visualize the capsule deformation. (a) q = 0.6, (b) q = 0.4. (Wang et al. 2017).

Collaborators

Johann Walter, Coupling of boundary integral and finite element methods: application to the flow of spherical and ellipsoidal capsules, PhD Thesis, UTC, December 2009.
Xuqu Hu, Numerical simulation of the fluid-structure interactions of capsules flowing in a three-dimensional channel, PhD thesis, UTC, March 2013.
Toshi Omori, PhD Thesis, Tohoku University, Sendai (Japan), April 2012.
Etienne Foessel, Numerical simulation of capsules in simple shear flow: effect of viscosity contrast, Master Thesis, July2010.
Claire Dupont, Motion of an ellipsoidal capsule in shear flow, Master Thesis, September 2011.
Jean-Baptiste Bourjade, Modelling of bending effects for capsules in flow, Master Thesis, July 2011.
Claire Dupont, Dynamics of capsules in flow, Ecole Polytechnique Palaiseau, PhD Thesis, December 2014.
Fabien Delahaye, Dynamics of a red blood cell in shear flow. Master Thesis, July 2013.
Benjamin Sévénié, Microfluidic flows of capsules, UTC, PhD Thesis, June 2016.
Zhen Wang (PhD student), Microcapsules flowing in bifurcated channel, Institute of Bioengineering, Queen Mary University of London (UK).
Ziqiang Zou (Master Student), Lattice-Boltzmann-Finite Element coupling to simulate capsules in flow.
Bruno Sarkis (PhD student), Dynamics of capsules in flow, UTC – UMPC Paris.
Xingyi Wang (PhD student), Dynamic behavior of microcapsule flowing through microchannel, UTC, PhD Thesis, May 2021.
Nicolas Grandmaison (PhD student), Fluid structure interaction modelling of capsules at the limit of rupture,UTC, PhD Thesis, December 2021.
Dr. Carlos Quesada Granja (Postdoc), Modelling of capsule deformation

• a.salsac@utc.fr
• +33 (0)3 44 23 73 38
• Biomechanics and Bioengineering Laboratory
  Université de Technologie de Compiègne
  CS 60319
  60203 Compiègne
  FRANCE